Overview and Objective
When comparing sizes of objects, it is common to make a statement such as one object is twice as large as another object. In this activity, students will discuss the importance of clarifying if the size comparison is based on length, area, or volume by exploring that the length, area, and volume of similar objects do not grow or shrink using the same scale factor.
Students also learn that this property is called Square-Cube Law by discussing its effects on cells, organisms, and animals.
Warm-Up
Enlargement is a transformation that changes the size of an object by a scale factor. Share this polypad with students and have them use the custom polygon to enlarge the square. Click here to learn how to share polypads with students and how to view their work and click here to learn more about using the custom polygon tile.
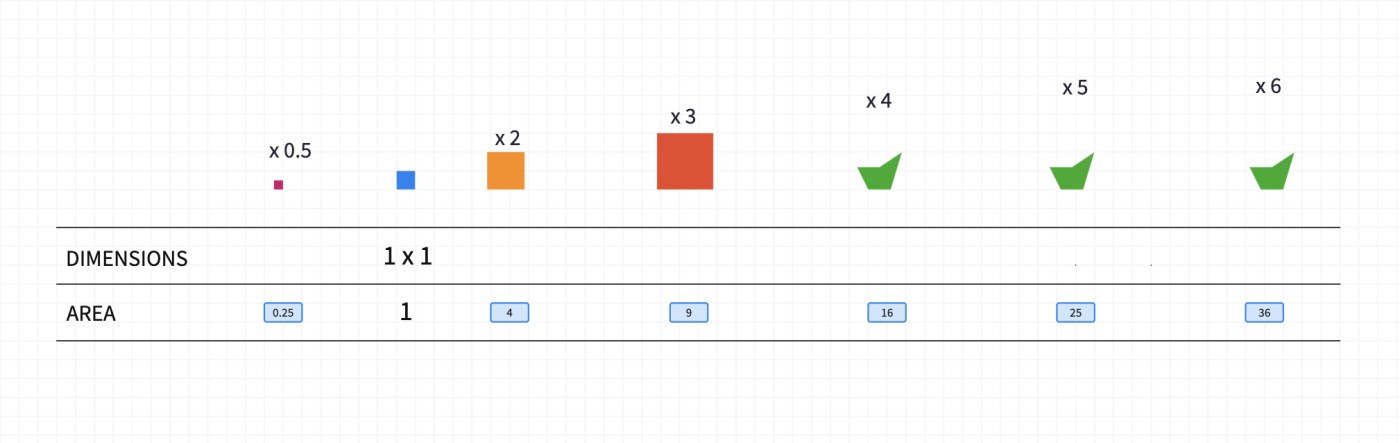
Take some time to discuss that when the length of a square is doubled, the area becomes four times bigger, when it is tripled, the area becomes 9 times bigger and so on.
Main Activity
Share this canvas with students and let them create the nets of cubes using given squares. After creating each net, they will use the "Fold Net" button to create the cubes.

Encourage students to use a table to record the side length, surface area, and volume of each cube. Discuss as a class at what side length of square the area became equal to the volume, and what happened after that point? Proportionately, which grows faster: surface area or volume?
Let them express the area and volume algebraically using the equation tool. Then, sketch the graphs of area and volume functions by dragging the equations on to the coordinate plane.
After discussing the graphs, invite students to add a column to their table to record the ratio of surface area to volume. Discuss what they notice and wonder. Which cube has the most surface area in proportion to its volume?
Some students may come with the ratio of as a general form. As the side length increases, the volume becomes much bigger numerically with respect to the area.
Explore what happens to the SA:V ratio with a scale factor of less than 1. Try examples of 0.5 and 0.25. It might be worth clarifying that if two shapes are similar by a scale factor , then their areas are proportional with a scale factor of and their volumes are proportional with a scale factor of . At this point, you may further discuss the importance of clarifying if the size comparison is based on length, area, or volume for similar shapes.
Closure
Share with students that this property is called the square-cube law. It is a mathematical principle, applied in a variety of scientific fields, which describes the relationship between the volume and the surface area as a shape's size increases or decreases.
It was first described in 1638 by Galileo Galilei in his book of Two New Sciences. It helps explain phenomena including why large mammals like elephants have a harder time cooling themselves than small ones like mice, and why building taller and taller skyscrapers is increasingly difficult.
More on the Biology Connection
Cubes can be used to serve as a model cell. In order for cells to survive, they must exchange nutrients and waste with their environment using the cell membrane that covers the surface of the cell. When the volume of the cell increases, more reactions will be needed. As a cell grows, its SA:V decreases. As SA:V decreases, the reactions on the surface of the cell fail to meet the needs of its volume. At this point the cell cannot get any larger.
For example, if a human becomes 10 times taller, wider, and longer, the skin would cover 100 times more surface area, but the volume (therefore the weight) would be 1,000 times bigger. It means only 10 times bigger bones needs to carry 1000 times bigger weight. Although science fiction writers have fun playing with the idea, any giant animal or human would break its legs with the first step it took .
To close the lesson, ask students to think about how flattening an object while keeping the volume constant impacts the surface to volume ratio?
- Why leaves are very thin and flat? Why do desert plants generally have smaller leaves?
- For animals, heat loss occurs only at the exposed surfaces. If animals need to maintain a constant body temperature, how can you explain the large, almost flat ears of elephants or fur covered skins of mice?
Support and Extension
For students ready for additional extension in this lesson, consider asking the following question:
If you cut a cube in half, how does the volume, surface area, and SA: V change comparing the original?
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account. Click here to learn how to share Polypads with students and how to view their work.