Puzzle Board
Instructions
Seven of these coins are real gold and one is a fake. The fake coin is known to be lighter than a real gold coin. Can you determine which coin is the fake in only 2 weighings of the coins? You can only use these 8 coins and the balance scale.
Hint
If there were only three identical coins, only one weighing can help you to determine the counterfeit one.

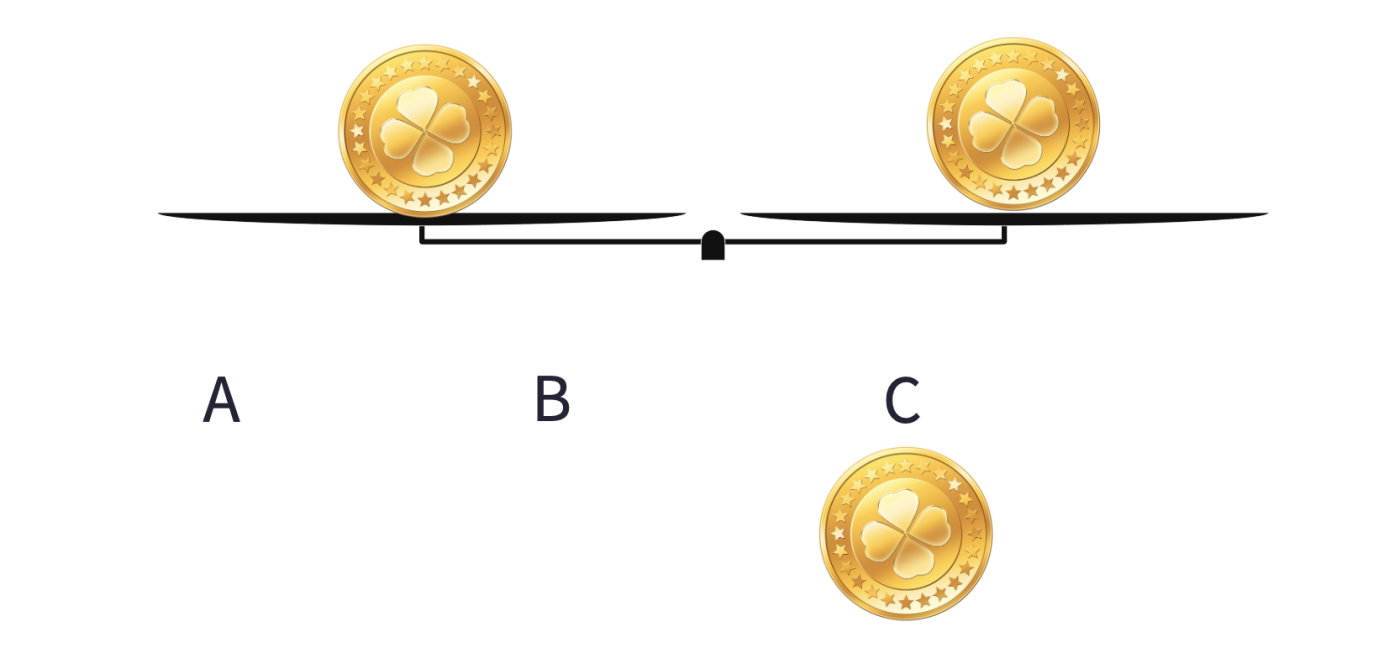
Think of placing coins A and B on the balance scale.
- If A is lighter than B then certainly, A is the counterfeit coin.
- If A is heavier than B, B is certainly the counterfeit coin.
- What happens if they weigh the same?
Solution
First, coins are grouped in 3s. The third group only has the remaining two coins.
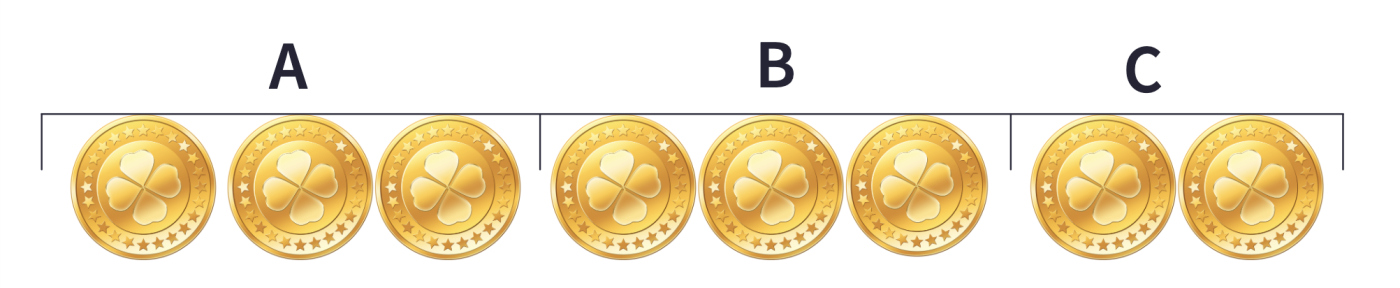
Then, place the coins in sets A and B on the balance.
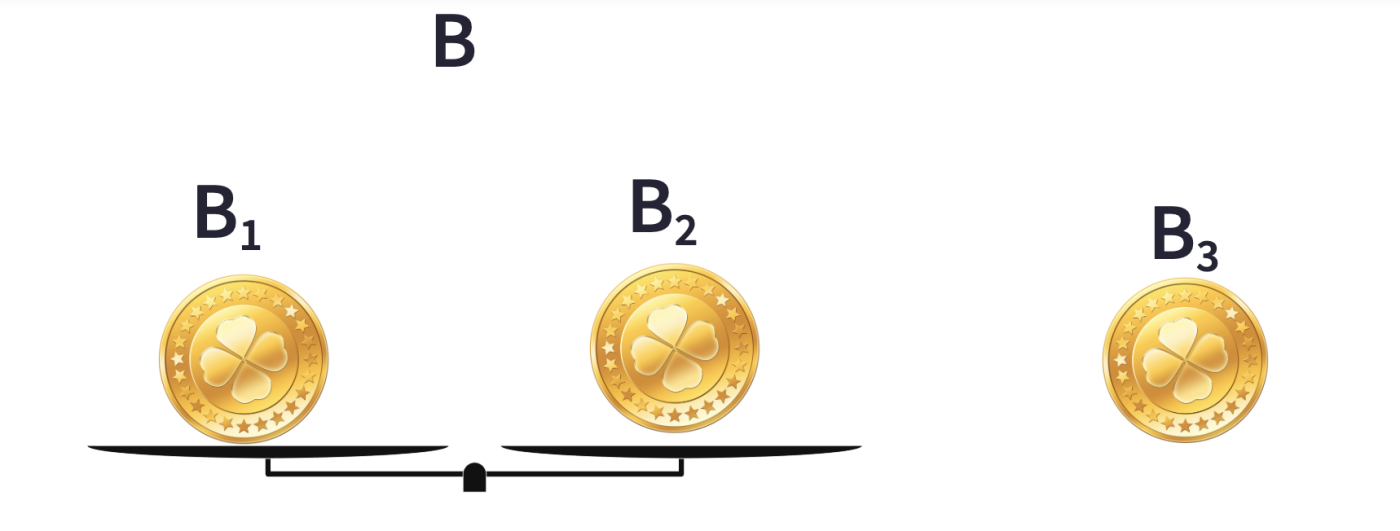
In the first scenario, if the coins in one set are lighter than the other one, we know that the fake coin is in that set, so we continue with that set.

- Use any two coins in the lighter set (In this example, use the coins in set B), by using the logic given in the hint.
- If one of the coins you choose (In this example and ) is lighter than one another, you found the counterfeit coin.
- If there is a balance between the coins you choose then, is the counterfeit coin.
So in a total of only 2 weightings, you can determine the fake coin!
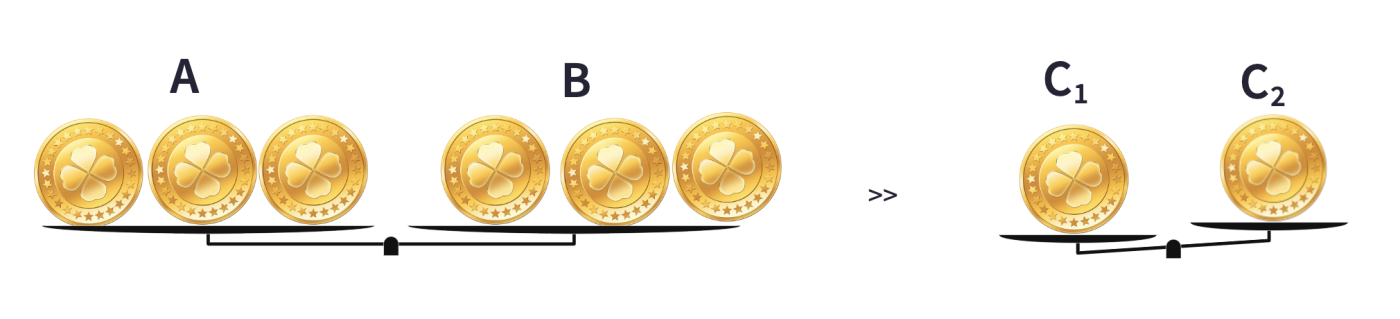
In the second scenario, if Sets A and B weigh the same on the first scale, then you would know that the counterfeit coin is in Set C. Since Set C has two coins, again by using the balance scale one more time, we can determine the fake coin.
More on the Gold Coin Puzzle
This famous logic puzzle has different variations where the total number of coins is different or instead of one fake one, there can be only one true gold coin that you suppose to identify Determine the least number of weighings needed for 4, 5, 7, 9 … coins and generalize your findings.
| , | , | , | , | , | , | , | , | , | |
| , | , | , | , | , | , | , | , | , |
When you know that the fake coin is lighter than the genuine ones, you can use the same number of weighings “n”, up to coins. For instance, you can find the fake coin in 2 weightings () up to coins.
Next
If you like this puzzle, try this one!