Dreiecke und TrigonometrieEigenschaften von Dreiecken
Fangen wir ganz einfach an: Ein Dreieck ist eine geschlossene Figur mit drei Seiten (die
Wir können Dreiecke nach der Größe ihrer Winkel einteilen:
Ein rechtwinkliges Dreieck hat einen
Ein stumpfwinkliges Dreieck hat einen
Ein spitzwinkliges Dreieck hat
Aus Gründen der Übersichtlichkeit beschriften wir Dreiecke immer auf die gleiche Weise. Die Eckpunkte werden mit Großbuchstaben A, B und C, die Seiten mit Kleinbuchstaben a, b und c und die Winkel mit griechischen Buchstaben
Die Seite, die gegenüber dem Eckpunkt A liegt, ist mit a, und der Winkel, der direkt bei A anliegt, mit
Seitenhalbierende (Schwerlinien)
Hier siehst du ein Dreieck sowie die
Eine
Es scheint, dass sich die Seitenhalbierenden immer
Schwerlinien (Seitenhalbierende) teilen sich immer im Verhältnis 2:1. Für jede der drei Schwerlinien ist der Abstand vom Eckpunkt zum Schwerpunkt immer
Der Schwerpunkt ist auch der “Balancierpunkt” eines Dreiecks. Zeichne ein Dreieck auf einen Karton, schneide es aus und finde die drei Seitenhalbierenden (Schwerlinien). Wenn du genau gearbeitet hast, kannst du das Dreieck nun auf der Bleistiftspitze ausbalancieren oder es ganz waagrecht an einem Stück Schnur aufhängen, die an seinem Schwerpunkt befestigt ist:
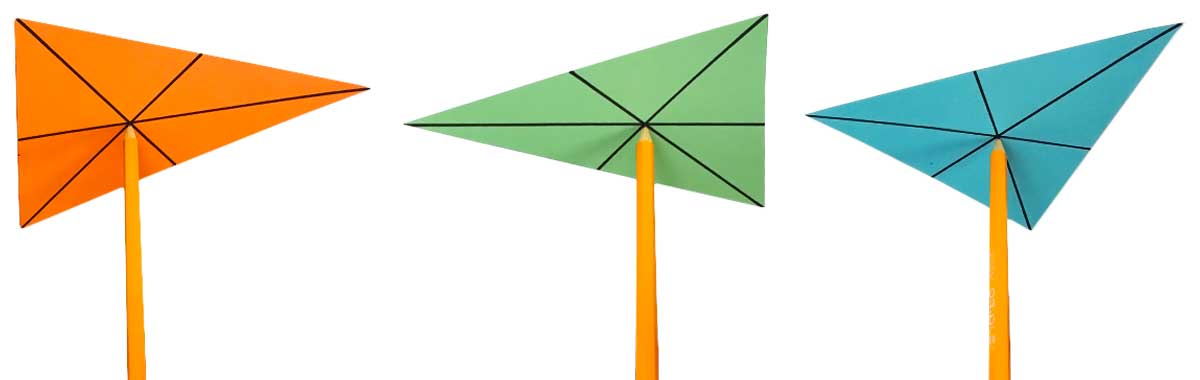
Das funktioniert, weil das Gewicht des Dreiecks gleichmäßig um den Schwerpunkt verteilt ist. In der Physik wird dieser Punkt oft als Massenschwerpunkt bezeichnet. // Any straight line that goes through the centroid divides the triangle into two // parts that have exactly the same area. Move the blue point in the // figure on the right. The red and green areas will always have the same area.
Streckensymmetralen und Umkreis
Erinnere dich, dass die
Zeichne die Streckensymmetrale aller drei Seiten dieses Dreiecks. Um die Streckensymmetrale einer Seite des Dreiecks zu zeichnen, klicke auf einen Eckpunkt und ziehe ihn einfach zum anderen Endpunkt der Seite.
Wie zuvor schneiden sich die drei Streckensymmetralen in einem einzigen Punkt. Und wieder hat dieser Punkt eine besondere Eigenschaft.
Jeder Punkt auf einer Streckensymmetrale hat den gleichen Abstand zu den beiden Endpunkten der Strecke, die er halbiert. So hat beispielsweise jeder Punkt auf der blauen Symmetrale den gleichen Abstand zu den Punkten A und C und jeder Punkt auf der roten Symmetrale den gleichen Abstand zu den Punkten
Der Schnittpunkt liegt auf allen drei Senkrechten, daher muss er den gleichen Abstand zu allen drei
Das bedeutet, dass wir einen Kreis um ihn herum zeichnen können, der genau durch alle Eckpunkte geht. Dieser Kreis wird als
Das heißt, dass wenn du drei Punkte gegeben hast, du den Umkreismittelpunkt benutzen kannst, um den Kreis zu finden, der durch alle diese drei Punkte geht. (Es sei denn, die Punkte sind
Winkelsymmetralen und Inkreis
Du hast jetzt wahrscheinlich den Dreh raus: Wir wählen eine bestimmte Geradenkonstruktion aus, führen diese dreimal für alle Seiten/Winkel der Dreiecke aus, und versuchen dann herauszufinden, was das Besondere am Schnittpunkt der Geraden ist.
Erinnere dich, dass die
Auch hier schneiden sich alle drei Linien in einem Punkt. Du hast so etwas wahrscheinlich erwartet, aber es ist wichtig zu beachten, dass es eigentlich keinen offensichtlichen Grund gibt, warum dies passieren sollte - außer dass Dreiecke eben sehr spezielle Figuren sind!
Punkte, die auf einer Winkelsymmetralen liegen, haben den gleichen Abstand zu den beiden Linien, die den Winkel bilden. Zum Beispiel hat jeder Punkt auf der blauen Symmetrale den gleichen Abstand von Seite a und Seite c, und jeder Punkt auf der roten Symmetrale hat den gleichen Abstand von den Seiten
Der Schnittpunkt liegt auf allen drei Symmetralen. Daher muss er den gleichen Abstand von allen drei
Das bedeutet, dass wir einen Kreis um ihn herum zeichnen können, der innerhalb des Dreiecks liegt und seine drei Seiten nur in jeweils einem Punkt berührt. Dieser Kreis wird als Inkreis des Dreiecks bezeichnet, und sein Mittelpunkt als Inkreismittelpunkt.
Fläche und Höhen
Die Berechnung der Fläche eines
Die Länge des Rechtecks ist gleich der Länge der unteren Seite des Dreiecks (die als Grundseite (Basis) bezeichnet wird). Die Höhe des Rechtecks ist der senkrechte Abstand von der Basis zum gegenüberliegenden Eckpunkt.
Die Höhe teilt das Dreieck in zwei Teile. Beachte, dass die zwei Lücken im Rechteck genau so groß sind wie die beiden entsprechenden Teile des Dreiecks. Das bedeutet, dass das Rechteck
Wir können die Fläche des Rechtecks leicht herausbekommen, und die Fläche des Dreiecks muss dann also halb so groß sein:
Um die Fläche eines Dreiecks zu berechnen, kannst du eine der drei Seiten als Basis auswählen und dann die entsprechende Höhe bestimmen, d.h. die Strecke, die
In Dreiecken spricht man von der
Wie die
Bei
Bei
Bei