Dreiecke und TrigonometrieDer Satz des Pythagoras
Wir sind nun an einem wichtigen Punkt in der Geometrie angelangt - wir sind in der Lage, einen der berühmtesten
Der Satz des Pythagoras In jedem rechtwinkligen Dreieck ist das Quadrat der Länge der Hypotenuse (die Seite, die dem rechten Winkel gegenüberliegt) gleich der Summe der Quadrate der anderen beiden Seiten. Mit anderen Worten,
Umgekehrt gilt auch: Wenn für die drei Seiten eines Dreiecks

Rechte Winkel sind überall, und deshalb ist der Satz des Pythagoras so nützlich.
Hier siehst du eine 6 m lange Leiter, die an eine Wand gelehnt ist. Das untere Ende der Leiter ist 1 m von der Wand entfernt. Wie weit reicht sie die Wand hinauf?
Beachte, dass ein rechtwinkliges Dreieck gebildet wird, das aus der Leiter, der Wand und dem Boden besteht. Mit dem Satz des Pythagoras können wir das so schreiben:
Immer wenn du ein rechtwinkliges Dreieck gegeben hast und zwei seiner Seiten kennst, kannst du mit dem Satz des Pythagoras die dritte bestimmen.
Beweise für den Satz des Pythagoras
Der Satz des Pythagoras war den alten Babyloniern, Mesopotamiern, Indern und Chinesen bekannt - aber Pythagoras war wohl der erste, der einen formalen, mathematischen Beweis fand.
Es gibt tatsächlich viele verschiedene Möglichkeiten, den Satz des Pythagoras zu beweisen. Hier zeigen wir drei verschiedene Beispiele, die jeweils eine andere Strategie verwenden:
Neuanordnung
Schau dir die Abbildung rechts an. Das Quadrat hat die Seitenlänge
Nun ordnen wir die Dreiecke im Quadrat neu an. Das Ergebnis enthält noch immer die vier rechtwinkligen Dreiecke sowie zwei Quadrate mit der Fläche
Vergleicht man die Größe des roten Bereichs und der Umstellung, so sieht man, dass
Das ist genau der gleiche Beweis, den sich
Algebra
Hier haben wir die gleiche Skizze wie zuvor, aber diesmal verwenden wir Algebra anstatt einer Neuanordnung, um den Satz des Pythagoras zu beweisen.
Das große Quadrat hat eine Seitenlänge von
Es besteht aus vier Dreiecken, mit einer Fläche von jeweils
Wenn wir alle diese Informationen zusammenführen, bekommen wir folgende Gleichung:
Und wieder erhalten wir den Satz des Pythagoras.
Ähnliche Dreiecke
Hier haben wir irgendein rechtwinkliges Dreieck. Wenn wir eine der Höhen einzeichnen, teilt sie das Dreieck in zwei kleinere Dreiecke auf, und sie teilt die Hypotenuse c in zwei kleinere Teile , die wir x und y nennen wollen.
Sehen wir uns die beiden kleineren Dreiecke getrennt an, damit klarer wird, wie sie zusammenhängen…
Beide kleineren Dreiecke teilen sich einen Winkel mit dem ursprünglichen Dreieck. Beide haben auch einen rechten Winkel. Es gilt der WWW-Satz, dh alle drei Dreiecke sind
Jetzt können wir die Gleichungen verwenden, die wir bereits über ähnliche Vielecke kennen:
Aber erinnere dich, dass c = y + x. Wir setzen ein und erhalten
Und damit haben wir ein weiteres mal den Satz des Pythagoras bewiesen!
Vieles über Pythagoras' Leben ist unbekannt, und es sind keine Originalschriften seines Werkes erhalten geblieben. Er gründete einen religiösen Kult, die Pythagoräer, der eine Art “Zahlenverehrung” praktizierte. Sie glaubten, dass alle Zahlen ihren eigenen Charakter haben, und folgten einer Vielzahl anderer bizarrer Bräuche.
Den Pythagoräern werden viele mathematische Entdeckungen zugeschrieben, darunter das Auffinden der ersten
“Pythagoräer feiern den Sonnenaufgang” von Fjodor Bronnikow
Abstände berechnen
Eine der wichtigsten Anwendungen des Satzes des Pythagoras ist die Berechnung von Abständen.
Auf der rechten Seite siehst du zwei Punkte in einem Koordinatensystem. Wir könnten ihren Abstand mit einem Lineal messen, aber das ist nicht besonders genau, stattdessen versuchen wir es mit Pythagoras.
Wir können leicht den horizontalen Abstand entlang der x-Achse und den vertikalen Abstand entlang der y-Achse abzählen. Wenn wir diese beiden Linien einzeichnen, erhalten wir ein rechtwinkliges Dreieck.
Mit Pythagoras,
Diese Methode funktioniert für zwei beliebige Punkte:
Die Abstandsformel Wenn du zwei Punkte mit den Koordinaten (
Pythagoräische Tripel
Als du die
Ein berühmtes Beispiel ist das 3-4-5 Dreieck. Da
Die alten Ägypter wussten nichts über den Satz von Pythagoras, aber sie wussten etwas über das 3-4-5 Dreieck. Beim Bau der Pyramiden verwendeten sie geknotete Seile der Längen 3, 4 und 5, um perfekte rechte Winkel zu messen.
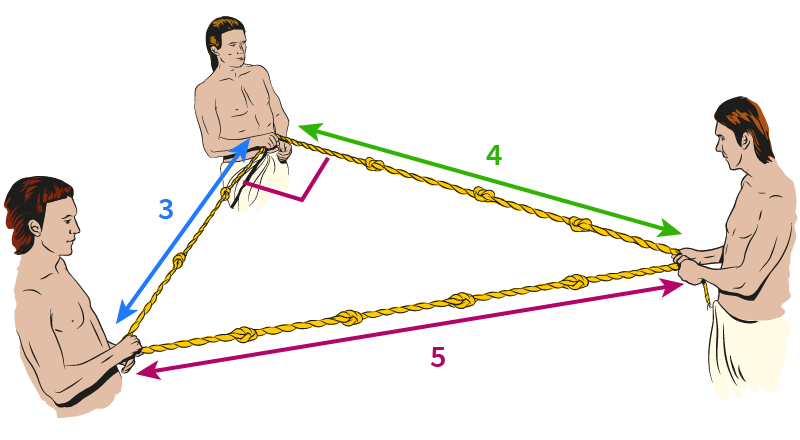
Drei Zahlen wie diese werden als
Wir können uns diese Tripel als Gitterpunkte in einem Koordinatensystem vorstellen. Für ein gültiges Pythagoräisches Tripel muss der Abstand vom Ursprung bis zum Gitterpunkt eine ganze Zahl sein. Kannst du mit dem untenstehenden Koordinatensystem weitere Pythagoräische Tripel finden?
Erkennst du ein Muster in der Verteilung dieser Punkte?