FraktaleEinführung
Wenn du dich in der Natur umschaust, hast du vielleicht komplizierte Pflanzen wie diese bemerkt:


Dieser Farn besteht aus vielen kleinen Blättern, die von einem größeren abzweigen.


Dieser Romanesco-Brokkoli besteht aus kleineren
Anfangs erscheinen diese wie hochkomplexe Formen - aber wenn du genauer hinschaust, wirst du feststellen, dass beide einem relativ einfachen Muster folgen: Alle Einzelteile der Pflanzen sehen genauso aus wie die gesamten Pflanze, nur kleiner. Das gleiche Muster wird in kleineren Maßstäben immer wieder wiederholt.
In der Mathematik nennen wir diese Eigenschaft Selbstähnlichkeit, und Formen, die sie haben, heißen
Um unsere eigenen Fraktale zu erstellen, müssen wir mit einem einfachen Muster beginnen und es dann in kleineren Maßstäben immer wieder wiederholen.
Eines der einfachsten Muster könnte ein Liniensegment sein, wobei zwei weitere Segmente an einem Ende abzweigen. Wenn wir dieses Muster wiederholen, haben diese beiden blauen Segmente auch zwei weitere Zweige an ihren Enden.
Du kannst die blauen Punkte verschieben, um die Länge und den Winkel aller Zweige zu ändern. Dann erhöhe die Anzahl der Iterationen mit
Abhängig von der Position der Zweige kannst du völlig unterschiedliche Muster erstellen - ähnlich wie der oben, ein oder . Was kannst du sonst noch finden?
Ein weiteres berühmtes Fraktal ist das
Beachte, wie die endgültige Form aus drei identischen Kopien von sich selbst besteht, und jede davon besteht aus noch kleineren Kopien des gesamten Dreiecks! Du könntest das Dreieck für immer vergrößern, und die Muster und Formen wiederholen sich immer weiter.
Die Pflanzen am Anfang dieses Kapitels sehen wie Fraktale aus, aber es ist eindeutig unmöglich, im wirklichen Leben echte Fraktale zu erstellen. Wenn wir das gleiche Muster immer wieder wiederholen, immer kleiner, gelangen wir schließlich zu Zellen, Molekülen oder Atomen, die nicht mehr geteilt werden können.
Mit Hilfe der Mathematik können wir jedoch über die Eigenschaften nachdenken, die echte Fraktale „haben“ würden - und diese sind sehr überraschend…
Fraktale Dimensionen
Lasst uns zunächst über die Dimension von Fraktalen nachdenken. Eine Linie hat die Dimension
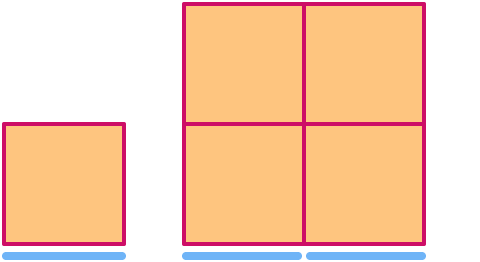
Ein Quadrat hat die Dimension
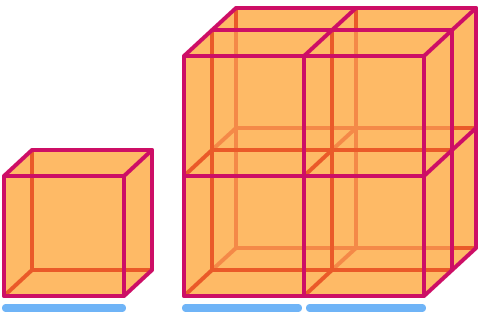
Ein Würfel hat die Dimension
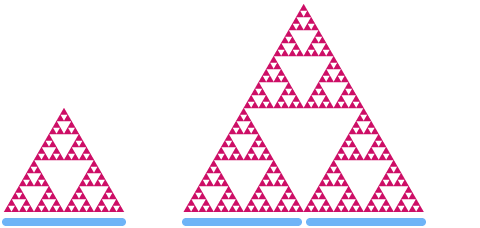
Schauen wir uns nun das Sierpinski-Dreieck an. Wenn wir es um den Faktor 2 skalieren, kannst du sehen, dass sich die „Fläche“ um den Faktor
Nehmen wir an, d ist die Dimension des Sierpinski-Dreiecks. Unter Verwendung des gleichen Musters wie oben erhalten wir
Aber warte ... wie kann etwas eine Dimension haben, die keine ganze Zahl ist? Es scheint unmöglich, aber dies ist nur eine der seltsamen Eigenschaften von Fraktalen. Dies ist es, was Fraktalen ihren Namen gibt: Sie haben eine Bruchdimension.
Mit jeder Iteration entfernen wir einen Teil der Fläche des Sierpinski-Dreiecks. Wenn wir dies unendlich oft tun könnten, wäre tatsächlich keine Fläche mehr vorhanden. Deshalb liegt das Sierpinski-Dreieck zwischen einem zweidimensionalen Fläche und einer eindimensionalen Linie.
Während viele Fraktale selbstähnlich sind, ist eine bessere Definition, dass Fraktale Formen sind, die eine nicht ganzzahlige Dimension haben.
Die Koch-Schneeflocke
Es gibt viele Formen in der Natur, die wie Fraktale aussehen. Wir haben bereits zu Beginn dieses Kapitels einige Pflanzen gesehen. Andere gute Beispiele sind Schneeflocken und Eiskristalle:
Um unsere eigene fraktale Schneeflocke zu erzeugen, müssen wir erneut ein einfaches Verfahren finden, das wir immer wieder anwenden können.
Beginnen wir wie beim Sierpinski-Dreieck mit einem einzigen gleichseitigen Dreieck. Anstatt bei jedem Schritt kleinere Dreiecke zu entfernen, fügen wir kleinere Dreiecke entlang der Kante hinzu. Die Seitenlänge jedes Dreiecks beträgt
Die resultierende Form heißt
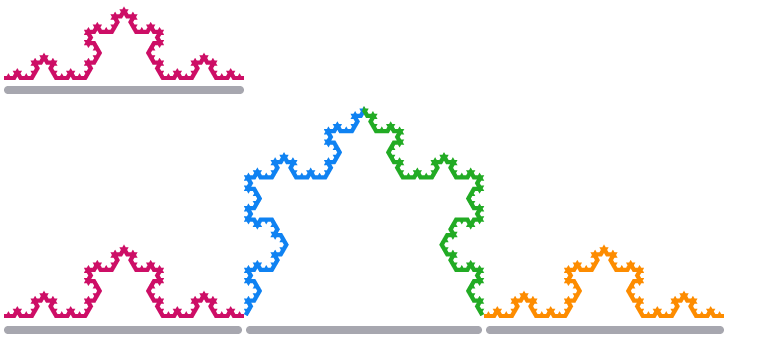
Wenn wir ein Kantensegment der Koch-Schneeflocke um den Faktor 3 skalieren,
Unter Verwendung der gleichen Beziehung zwischen Dimensionen und Skalierungsfaktoren wie oben erhalten wir die Gleichung
Fläche
Das Erstellen der Koch-Schneeflocken ist fast wie eine




Nach der ersten Iteration erhöht sich die Anzahl der neu hinzugefügten Dreiecke bei jedem Schritt um den Faktor
Nehmen wir an, das
Mit der Formel für die Summe der unendlichen
Umfang
Wir können auch versuchen, den Umfang der Koch-Schneeflocke zu berechnen. Wie wir bereits gesehen haben, ändert sich die Länge des Umfangs bei jedem Schritt um den Faktor
Dies bedeutet, dass wir wieder eine geometrische Reihe haben - aber in diesem Fall

Wenn dies nicht intuitiv erscheint, denke daran, dass wir den Umfang bei jedem Schritt mit
Es ist fast undenkbar, dass man eine Form mit einer endlichen Fläche und einem unendlichen Umfang haben können - aber dies ist nur eine der vielen unerwarteten Eigenschaften von Fraktalen.
Kannst du dir andere Möglichkeiten einfallen lassen, um deine eigenen Fraktale zu erstellen?
“My soul is spiralling on frozen fractals all around…”
Menger-Schwamm
Fraktale müssen nicht "flach" sein, wie viele der obigen Beispiele. Eines der bekanntesten Fraktale, die dreidimensional aussehen, ist der Menger-Schwamm, benannt nach dem Mathematiker
Wir beginnen mit einem festen Würfel und bohren wiederholt immer kleinere Löcher in seine Seiten. Jede neue Iteration von Löchern hat
Ein
Jetzt können wir versuchen, die Abmessung d des Menger-Schwamms genau wie für die Koch-Schneeflocke oben zu berechnen. In diesem Fall erhalten wir
Wenn du dir vorstellst, unendlich oft mehr und mehr Löcher auszuschneiden, ist kein tatsächliches Volumen mehr vorhanden. Deshalb ist der Würfel „nicht ganz“ dreidimensional!
Fraktale Küsten
Eines der Hauptmerkmale aller Fraktale, die wir bisher gesehen haben, ist, dass man für immer „hineinzoomen“ kann, und immer neue Muster findet. Um 1920 erkannte der britische Mathematiker
Man beginnt mit der Grundform des Landes und fügen beim Vergrößern Flusseinlässe, Buchten und Flussmündungen sowie einzelne Klippen, Felsen, Kieselsteine usw. hinzu:
Dies ist ein erhebliches Problem, wenn Sie versuchen, die Länge der Grenze eines Landes zu berechnen. Wie entscheidet man, wie weit die Ansicht vergrößert werden soll und welche Ecken und Winkel berücksichtigt werden sollen?
Eine Möglichkeit, die Länge der britischen Küste zu messen, besteht beispielsweise darin, ein langes Lineal zu nehmen, den ganzen Weg um die Strände herumzulaufen und dann alle Entfernungen zu addieren.
Wenn das Lineal
Wir können einfach mit immer kleineren Herrschern weitermachen, und jedes Mal wird unser Ergebnis für die Länge der Küste etwas länger. Genau wie bei der Koch-Schneeflocke scheint die britische Küste unendlich lang zu sein! Dies wird oft als Küstenparadoxon bezeichnet.
Einige Jahrzehnte später stieß der Mathematiker
Die Küste Großbritanniens sieht sicherlich fraktal aus, ist aber nicht selbstähnlich wie andere Fraktale, die wir zuvor gesehen haben. Um seine Größe zu ermitteln, können wir es in ein Raster zeichnen und die Anzahl der Zellen zählen, mit denen es sich schneidet.
Anfangs gibt es 88 sich schneidende Zellen. Wenn wir die Küste um den Faktor 2 skalieren, gibt es 197 sich schneidende Zellen - mehr als doppelt so viele!
Die Größe der Küste hat sich um den Faktor
Wenn wir dies mit größeren Gittern wiederholen, stellen wir fest, dass die Dimension der britischen Küste tatsächlich ungefähr 1,21 beträgt. Mandelbrot erkannte, dass diese fraktale Dimension auch ein Maß für die Rauheit einer Form ist - ein neues Konzept, für das er wichtige Anwendungen in vielen anderen Bereichen der Mathematik und Naturwissenschaften fand.
Mehr Fraktale in Natur und Technologie
Während echte Fraktale in der Natur niemals auftreten können, gibt es viele Objekte, die fast wie wie Fraktale aussehen. Wir haben bereits Pflanzen, Schneeflocken und Küsten gesehen, und hier sind einige weitere Beispiele:
Gebirgszug in Zentralasien
Ganges-Delta in Indien
Blitze
Blutgefäße in der Netzhaut
Grand Canyon in den USA
Wolken
Alle diese Objekte mögen völlig zufällig erscheinen, aber genau wie Fraktale gibt es ein zugrunde liegendes Muster, das bestimmt, wie sie gebildet werden. Die Mathematik kann uns helfen, die Formen besser zu verstehen, und Fraktale finden Anwendung in Bereichen wie Medizin, Biologie, Geologie und Meteorologie.
Computergeneriertes fraktales Gelände
Wir können auch Fraktale verwenden, um realistische „Kopien“ der Natur zu erstellen, beispielsweise als Landschaften und Texturen, die in Videospielen oder computergenerierten Filmen verwendet werden. Das Wasser, die Berge und die Wolken in diesem Bild werden vollständig von einem Computer mit Hilfe von Fraktalen erstellt!
Und wir können diesen Prozess sogar umkehren, um digitale Bilder zu komprimieren und ihre Dateigröße zu reduzieren. Die ersten Algorithmen wurden in den 1980er Jahren von Michael Barnsley und Alan Sloan entwickelt, und neue werden noch heute erforscht.