FraktaleDie Mandelbrot-Menge

Alle Fraktale, die wir in den vorherigen Kapiteln gesehen haben, wurden mit einem Prozess der Iteration erstellt: Sie beginnen mit einem bestimmten Muster und wiederholen es dann immer wieder.

Dies ähnelt einem anderen Konzept in der Mathematik, das Sie zuvor gesehen haben: Mit rekursiven Sequenzen beginnen Sie mit einer bestimmten Zahl und wenden dann immer wieder dieselbe rekursive Formel an, um die nächste Zahl in der zu erhalten Reihenfolge.

Nehmen wir als Beispiel die rekursive Formel xn=xn−12 und zeichnen ihre Begriffe auf eine Zahlenlinie. Sie können den Wert von x0 ändern:

Beachten Sie, wie sich die resultierende Sequenz je nach Startwert x0 sehr unterschiedlich verhalten kann:

Bisher haben wir nichts Neues gelernt. Vor ungefähr einem Jahrhundert begannen Mathematiker jedoch zu untersuchen, was mit diesen Sequenzen passiert, wenn Sie komplexe Zahlen anstelle nur der reellen Zahlenlinie verwenden. Ihre Entdeckungen waren einige der überraschendsten und schönsten Ergebnisse in der gesamten Mathematik.

Julia Sets

Verwenden wir dieselbe Sequenz wie zuvor, xn=xn−12, jedoch auf der komplexen Ebene. Sie können die Position von x0 verschieben, um zu sehen, was mit den folgenden Begriffen passiert. Wenn die Sequenz so aussieht, als würde sie konvergieren, färben wir den entsprechenden Punkt in der Ebene in blau:

Wie Sie sehen können, konvergiert die Sequenz, solange x0 innerhalb des Einheitskreises outside the unit squareabove the x-axis liegt (der Kreis mit dem Radius 1, zentriert am Ursprung).

Lassen Sie uns die Dinge jetzt etwas schwieriger machen. Anstatt nur die vorherige Zahl zu quadrieren, fügen wir jedes Mal eine Konstante c hinzu (die eine beliebige komplexe Zahl sein kann). Mit anderen Worten, xn=xn−12+c. Glauben Sie, wir werden immer noch einen Konvergenzkreis bilden? Welche anderen Formen könnten wir Ihrer Meinung nach sehen? Weiter

In diesem Diagramm können Sie die Position von x0 sowie den Wert von c verschieben:

Die verschiedenen Formen, die durch Färben der Zahlen gebildet werden, heißen Julia Sets. Sie wurden unabhängig voneinander von zwei französischen Mathematikern, Gaston Julia und Pierre Fatou, um 1918 entdeckt.

Zu dieser Zeit gab es keine Computer, um zu visualisieren, wie Julia-Sets tatsächlich aussahen. Mathematiker wie Julia und Fatou konnten mathematisch über sie nachdenken, aber sie sahen immer nur grobe, handgezeichnete Skizzen, wie sie aussehen könnten.

Wir haben dieses Problem heute nicht - die Bilder unten zeigen alle verschiedene Julia-Sets. Die verschiedenen Farben zeigen an, wie schnell die Sequenz an diesem Punkt divergiert:

Weiter

Die Mandelbrot-Menge

Beim Erstellen der verschiedenen Julia-Mengen haben Sie möglicherweise bemerkt, dass es einige Werte von c gab, für die jede Sequenz divergiert, und die gesamte komplexe Ebene weiß bleibt. Einige Jahrzehnte nach Julia und Fatou versuchte eine neue Generation von Mathematikern abzubilden, wie diese Gebiete aussahen.

Im vorherigen Beispiel haben wir einen festen Wert für c ausgewählt und dann die Position von x0 geändert, um die Ebene einzufärben. Legen Sie nun den Wert von x0=0 fest und ändern Sie stattdessen den Wert von c.

Übermalen Sie die komplexe Ebene erneut, um den Bereich anzuzeigen, in dem die Sequenzen begrenzt bleiben. Welche Formen erwarten Sie zu erscheinen?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

Dieses Fraktal wird als Mandelbrot-Menge bezeichnet. Wenn es um 90 ° gedreht wird, sieht es fast aus wie eine Person mit Kopf, Körper und zwei Armen. Es wurde 1978 zum ersten Mal in einem Forschungsbericht der Mathematiker Robert Brooks und Peter Matelski definiert und gezeichnet:

Einige Jahre später verwendete Benoit Mandelbrot die leistungsstarken Computer von IBM, um eine viel detailliertere Visualisierung des Fraktals zu erstellen, das später nach ihm benannt wurde. Die ersten Ausdrucke sahen anders aus als erwartet - bis er feststellte, dass die an den Druckern arbeitenden Techniker die „Unschärfe“ an ihrem Rand bereinigten, vorausgesetzt, dass sie durch Staubpartikel oder Druckerfehler verursacht wurde und kein definierendes Merkmal von Fraktalen war ! Weiter

Wie alle Fraktale können wir die Mandelbrot-Menge für immer „vergrößern“ und auf jeder Skala neue Muster finden. Hier kannst du einen Teil der Mandelbrot-Menge vergrößern, der als Seepferdchen-Tal bezeichnet wird. Schwarze Punkte befinden sich innerhalb von der Mandelbrot-Menge, wo die Sequenz begrenzt ist. Farbige Punkte befinden sich außerhalb von der Mandelbrot-Menge, wo die Sequenz divergiert, und die verschiedenen Farben zeigen an, wie schnell es bis ins Unendliche wächst:

Scale: ${pow(scale)}

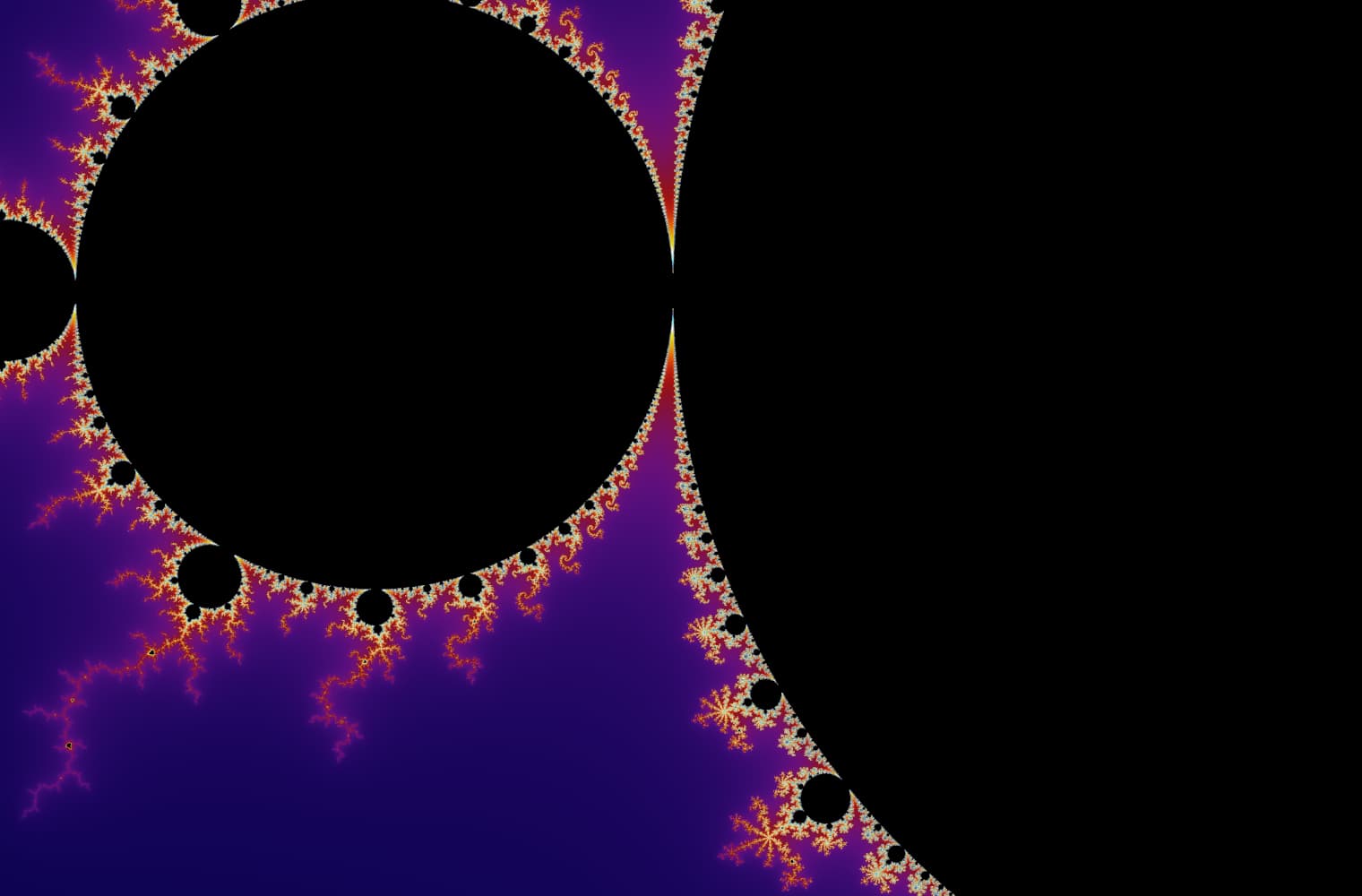
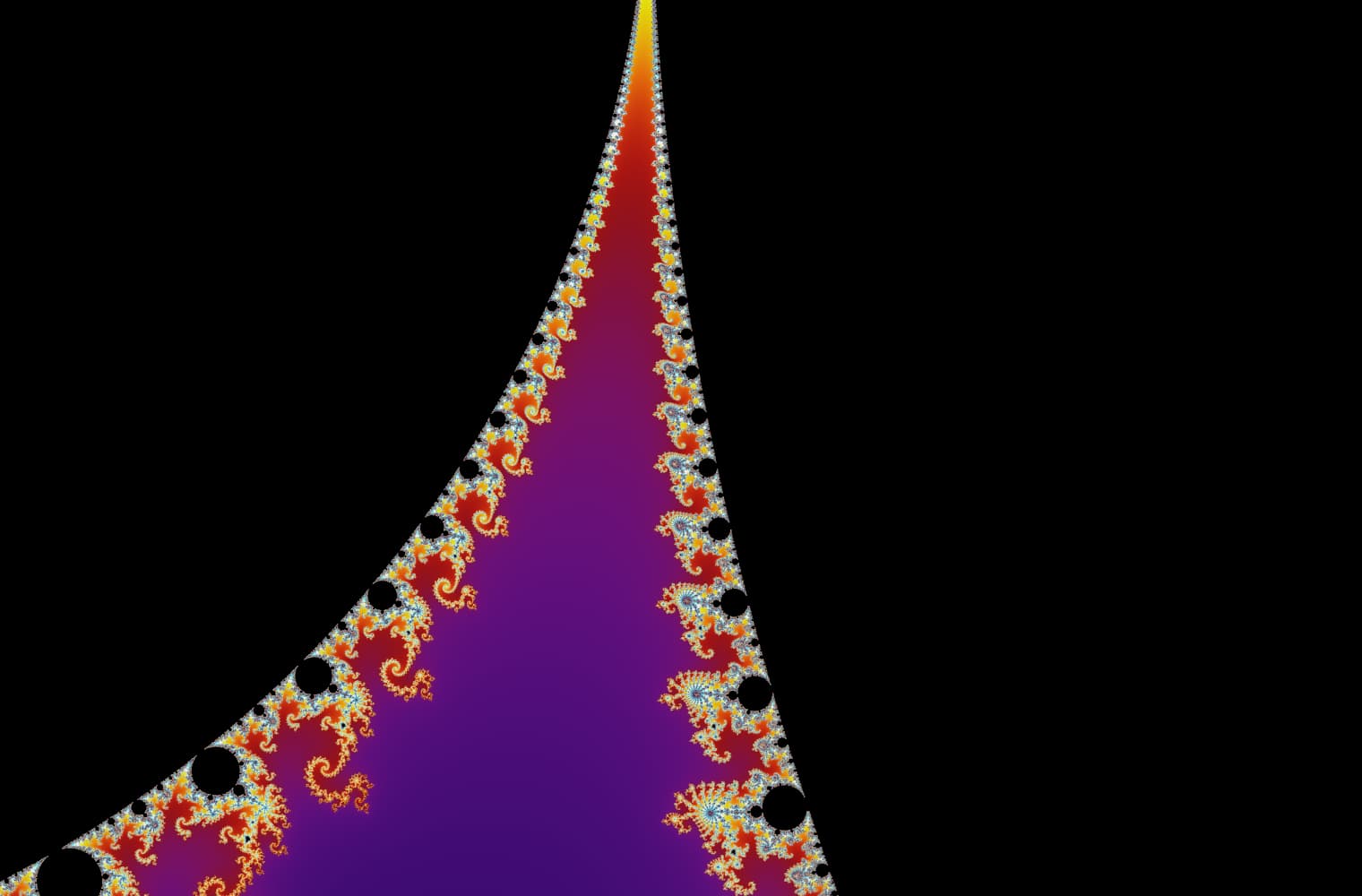
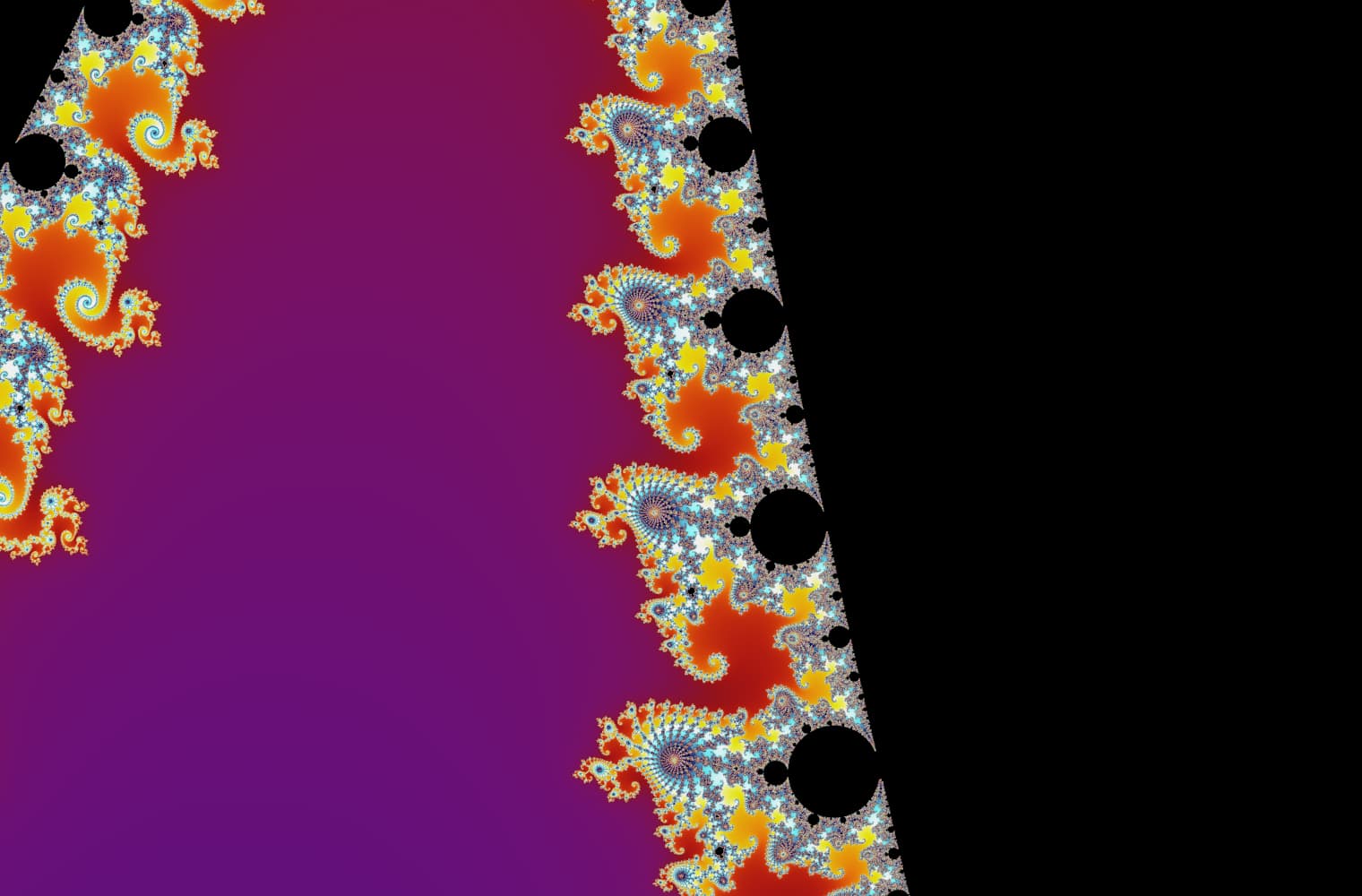
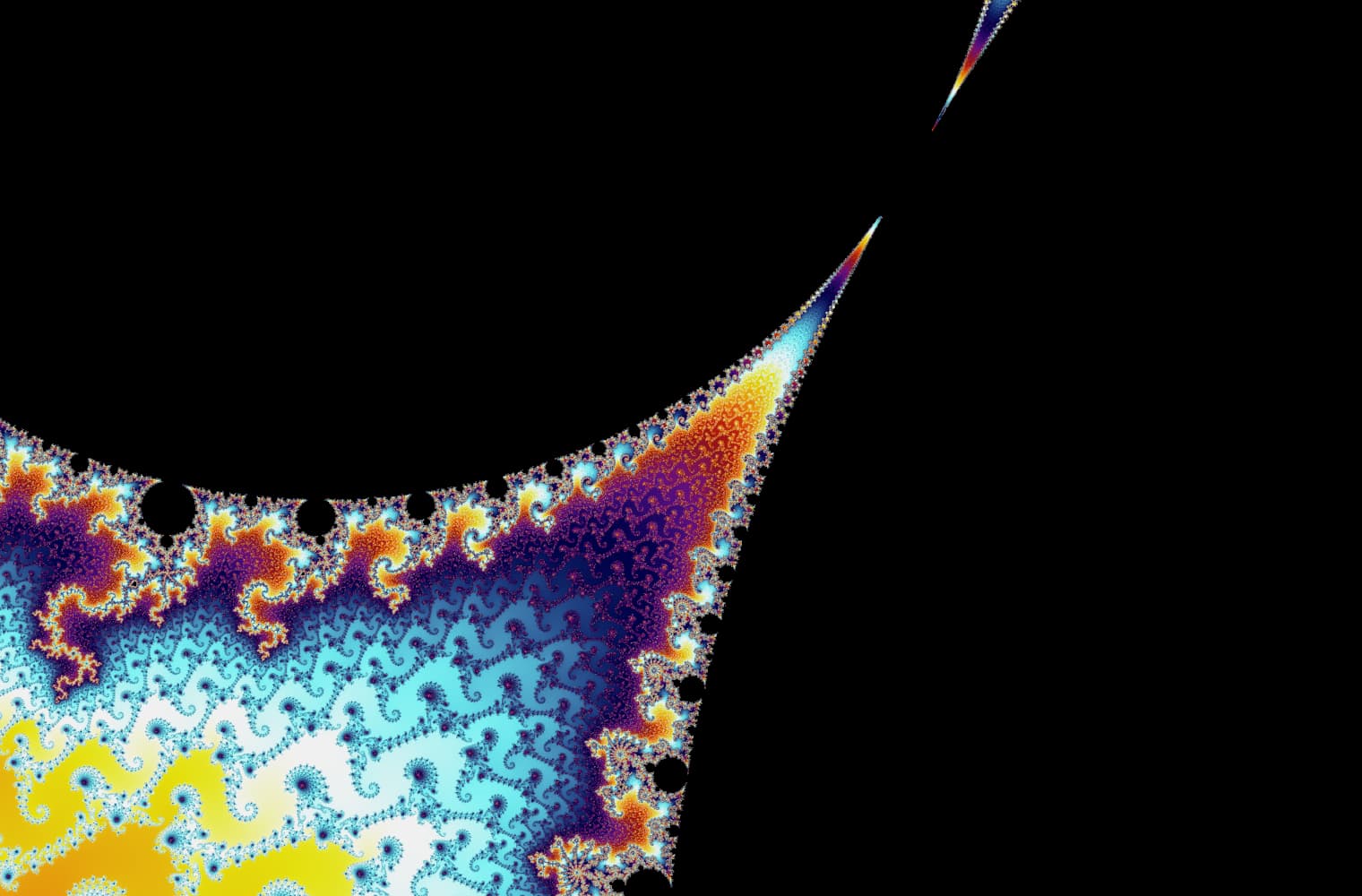
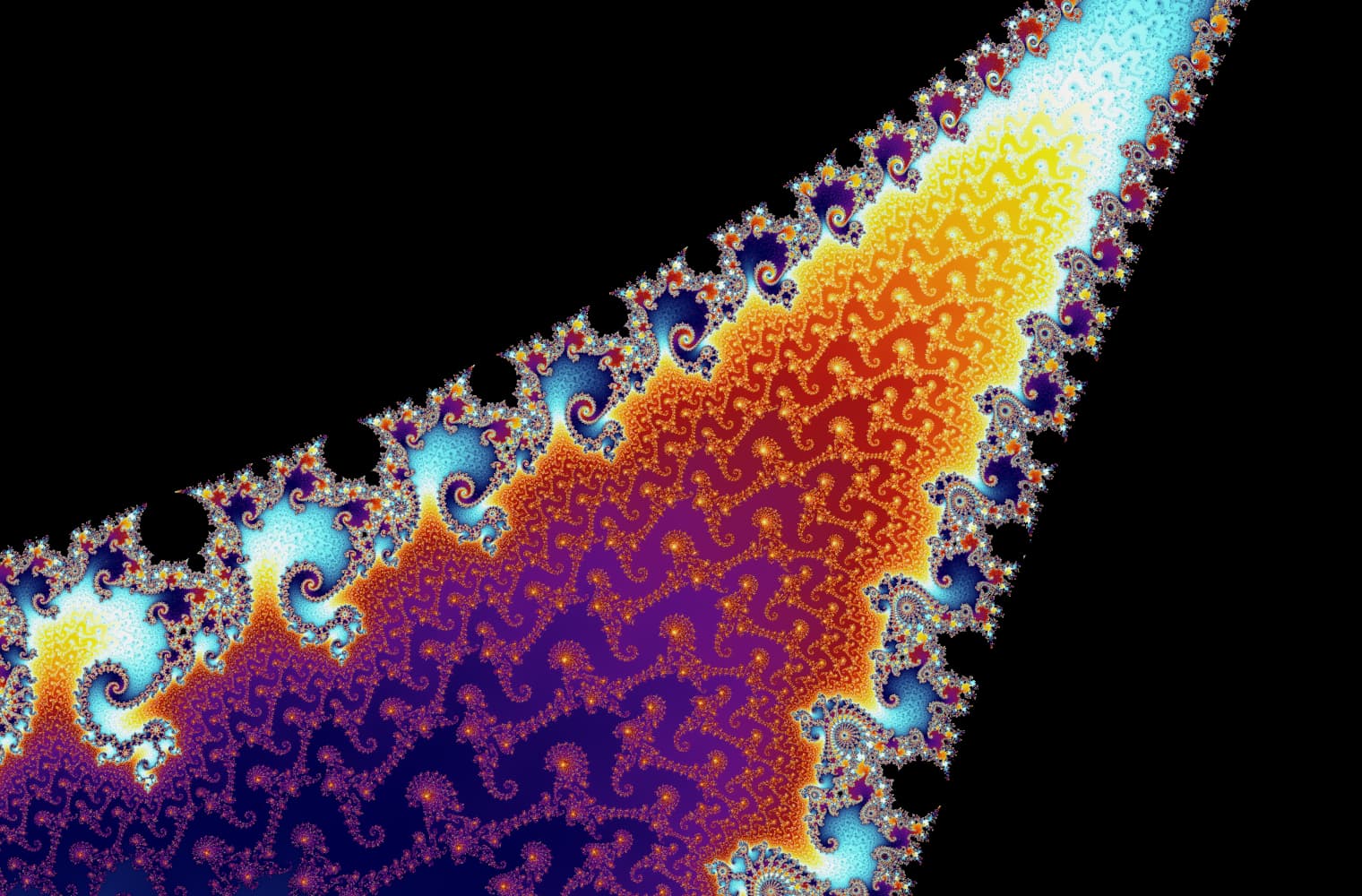
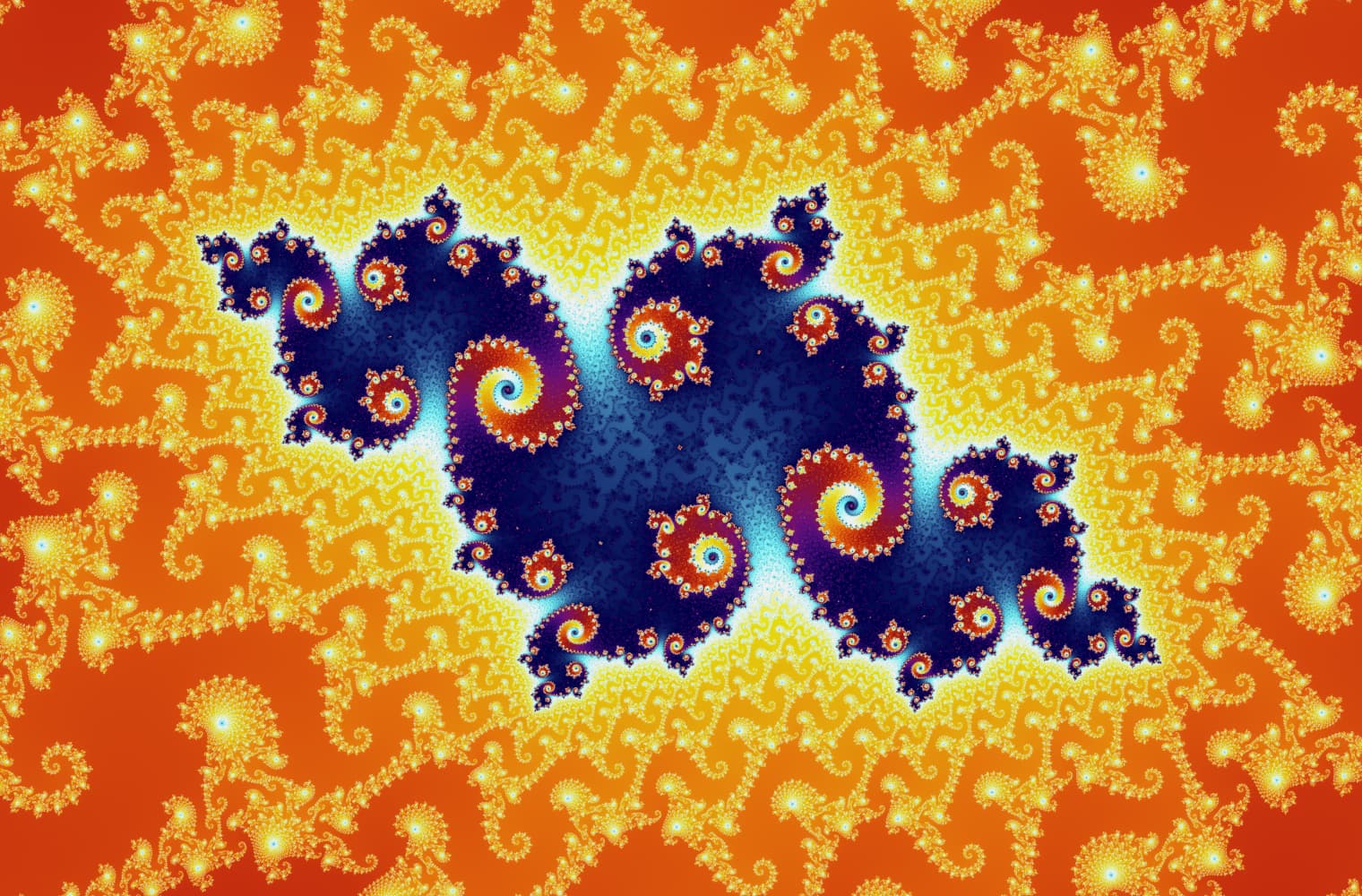
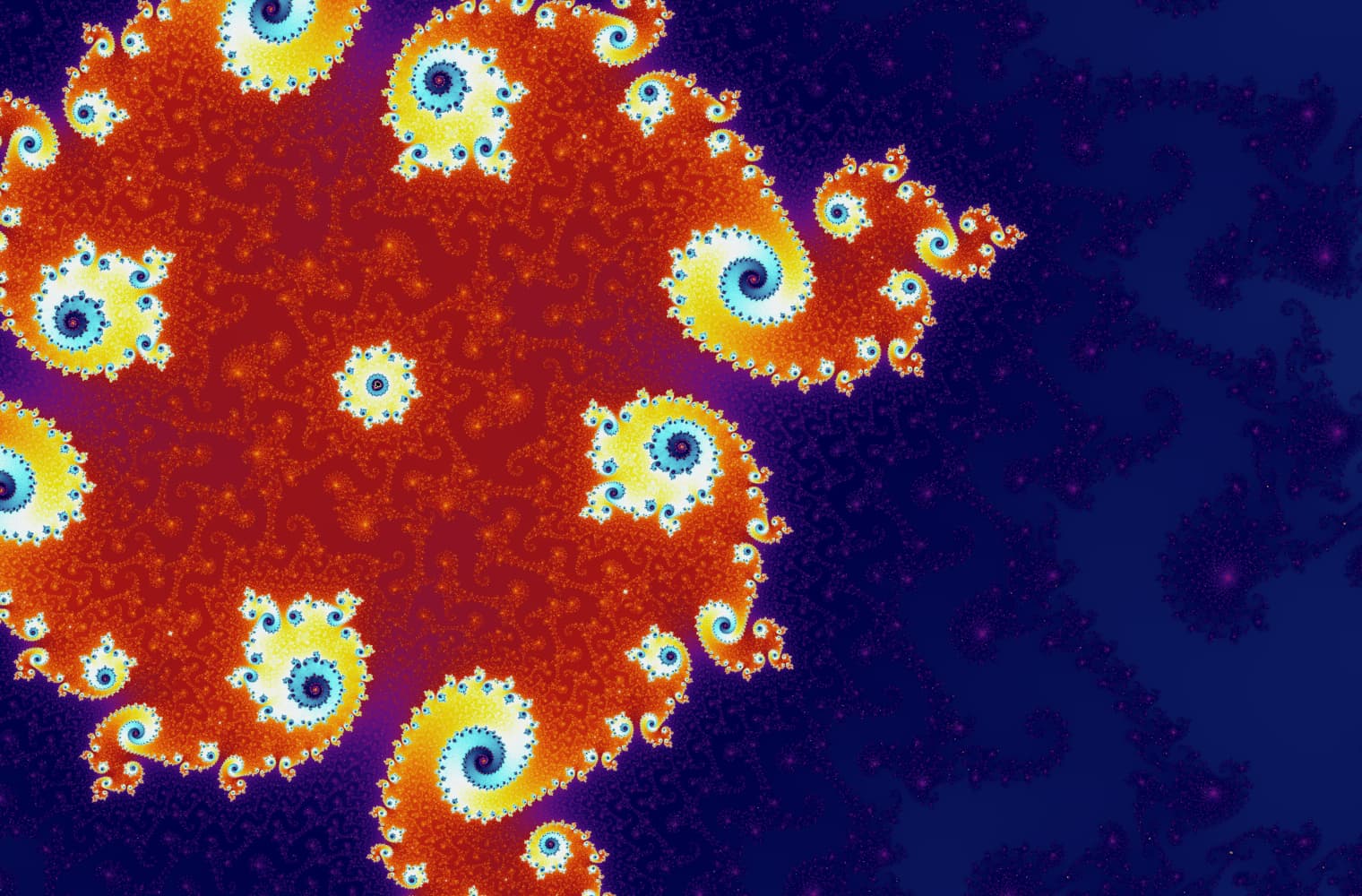
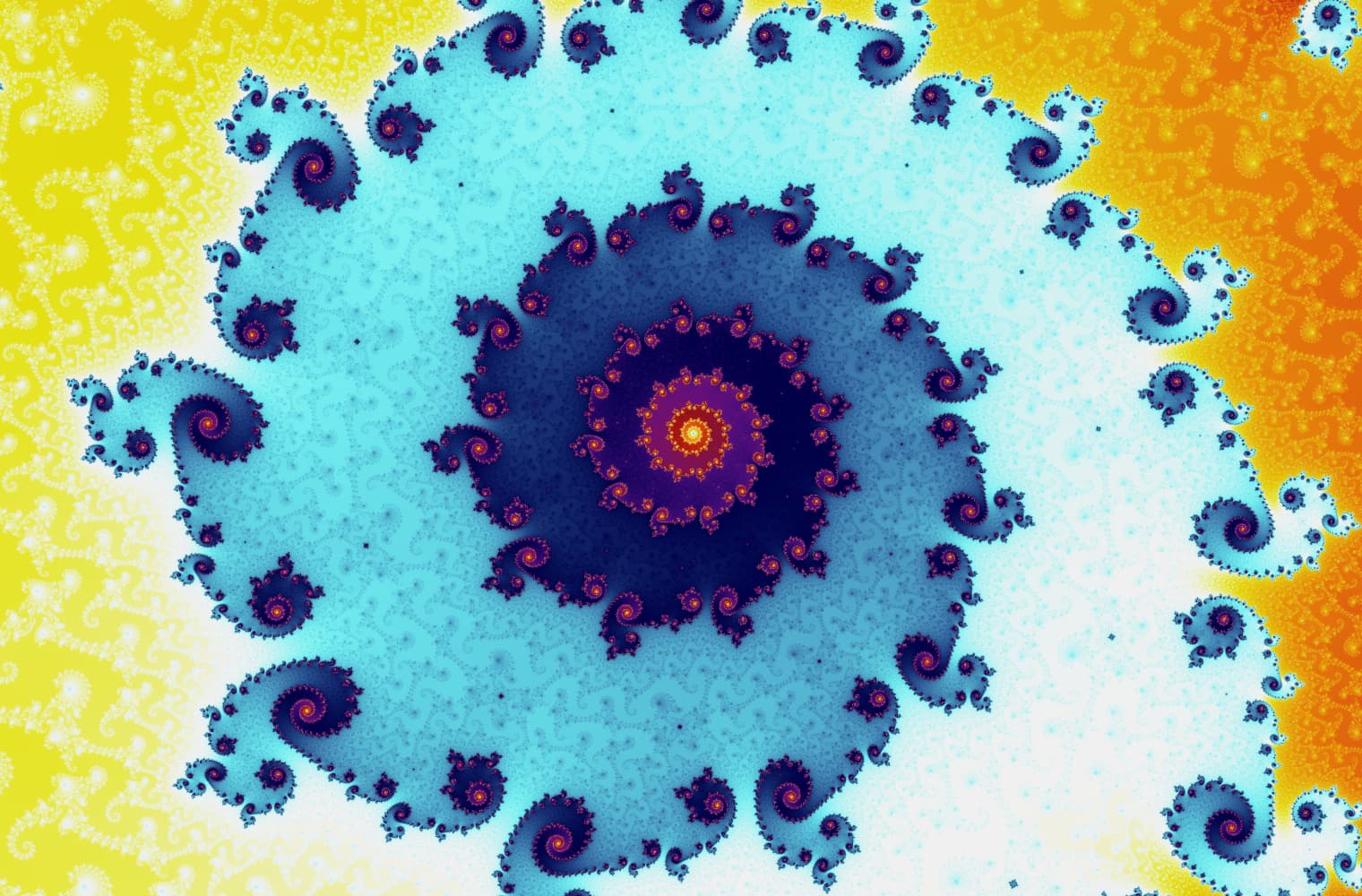
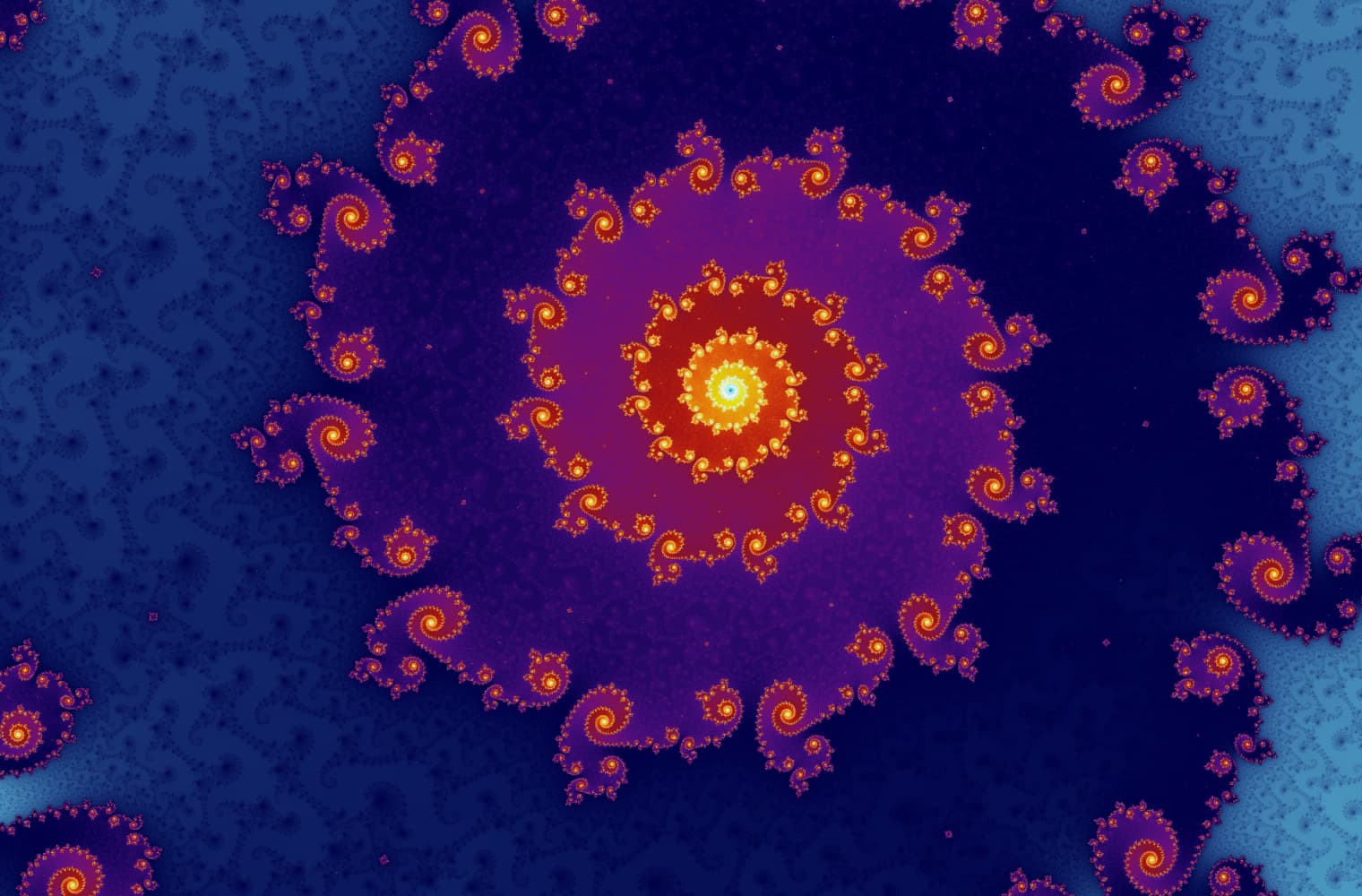
Dieser Schieberegler besteht aus 27 Einzelbildern bis zu einer Zoomstufe von über 14 Billiarden oder 254. Insgesamt dauerte das Rendern auf einem modernen Laptop fast 45 Minuten. Die Mandelbrot-Menge kann mit nur einer einfachen Gleichung xn=xn−12+c erstellt werden, ist jedoch unendlich komplex und atemberaubend schön.

Wenn Sie den Wert von c um die Mandelbrot-Menge verschieben, werden Sie möglicherweise eine merkwürdige Eigenschaft bemerken:

• Alle Sequenzen innerhalb des Hauptkörpers der Mandelbrot-Menge konvergierendivergereach an orbit zu einem einzelnen Punkt.
• Die Sequenzen innerhalb der großen Glühbirne oben erreichen eine Umlaufbahnconvergediverge , die aus Punkten besteht.
• Sequenzen in dieser kleineren Glühbirne haben Umlaufbahnen mit der Länge .

Jede Glühbirne hat eine Umlaufbahn unterschiedlicher Größe, wobei kleinere Glühbirnen immer mehr Punkte in ihrer Umlaufbahn haben. Die Größe dieser Umlaufbahnen hängt eng mit der Logistic Map zusammen, einem wichtigen Konzept in der Chaostheorie.