Folgen und MusterArithmetische und geometrische Folgen

Im Jahr 1682 beobachtete der Astronom Edmond Halley ein ungewöhnliches Phänomen: ein leuchtend weißes Objekt mit einem langen Schweif, das sich über den Nachthimmel bewegte. Es war ein Komet, ein kleiner, eisiger Felsbrocken, der durchs All fliegt und dabei eine Spur aus Staub und Eis hinterlässt.

Halley erinnerte sich daran, dass andere Astronomen schon viel früher ähnliche Kometen beobachtet hatten: einen im Jahr 1530 und einen anderen im Jahr 1606. Beachte, dass der Abstand zwischen zwei aufeinanderfolgenden Beobachtungen in beiden Fällen gleich groß ist: Jahre.

Bild des Halleyschen Kometen,
aufgenommen 1986 auf der Osterinsel

Halley kam zu dem Schluss, dass es sich bei allen drei Beobachtungen um denselben Kometen handelte, der heute Halleyscher Komet genannt wird. Er umkreist die Sonne und passiert die Erde etwa alle 76 Jahre. Er sagte auch voraus, wann der Komet das nächste mal sichtbar sein würde:

1530, 1606 +76, 1682 +76, 1758 +76, +76, +76, +76, …

Das Zeitintervall beträgt nicht immer exakt 76 Jahre: Es kann um ein oder zwei Jahre variieren, da die Umlaufbahn des Kometen durch andere Planeten gestört wird. Heute wissen wir, dass der Halleysche Komet bereits 240 v. Chr. von antiken Astronomen beobachtet wurde!

Darstellungen des Halleyschen Kometen im Laufe der Zeit: eine babylonische Tafel (164 v. Chr.), ein mittelalterlicher Wandteppich (1070er Jahre), ein Wissenschaftsmagazin (1910) und eine sowjetische Briefmarke (1986).

Eine andere Gruppe von Wissenschaftlern erforschte das Verhalten eines hüpfenden Tennisballs. Sie ließen den Ball aus einer Höhe von 10 Metern fallen und maßen seine Position zu verschiedenen Zeitpunkten. Bei jedem Aufprall verliert der Ball etwas von seiner ursprünglichen Höhe:

Die Wissenschaftler haben festgestellt, dass der Ball nach jedem Aufprall 20% seiner Höhe verliert. Mit anderen Worten: Die maximale Höhe bei jedem Aufprall beträgt 80 % des vorherigen Aufpralls. So konnten sie die Höhe jedes folgenden Aufpralls vorhersagen:

10, 8 ×0.8, ×0.8, ×0.8, 4.096 ×0.8, 3.277 ×0.8, 2.621 ×0.8, 2.097 ×0.8, …

Begriffe

Wenn du diese beiden Beobachtungen vergleichst, wirst du feststellen, dass es viele Ähnlichkeiten gibt: Bei der Folge des Halleyschen Kometen ist zwischen aufeinanderfolgenden Gliedern gleich, während bei der Folge von Tennisballsprüngen zwischen aufeinanderfolgenden Gliedern gleich ist.

Folgen mit diesen Eigenschaften haben einen besonderen Namen:

Eine arithmetische Folge hat eine konstante Differenz d zwischen aufeinanderfolgenden Gliedern.

Zu jedem Glied wird die gleiche Zahl addiert oder subtrahiert, um das nächste Glied zu erhalten.

Eine geometrische Folge hat ein konstantes Verhältnis r zwischen aufeinanderfolgenden Gliedern.

Jedes Glied wird mit der gleichen Zahl multipliziert oder dividiert, um das nächste Glied zu erhalten.

Hier haben wir einige unterschiedliche Folgen. Kannst du herausfinden, welche davon arithmetisch, geometrisch oder keines von beiden sind und welche Werte d und r haben?

2, 4, 8, 16, 32, 64, …

is , mit einem Verhältnis von .

2, 5, 8, 11, 14, 17, …

is , mit einer Differenz von .

17, 13, 9, 5, 1, –3, …

is , mit einer Differenz von .

2, 4, 7, 11, 16, 22, …

is .

40, 20, 10, 5, 2.5, 1.25, …

is , mit einem Verhältnis von .

To define an arithmetic or geometric sequence, we have to know not just the common difference or ratio, but also the initial value (called a). Here you can generate your own sequences and plot their values on a graph, by changing the values of a, d and r. Can you find any patterns?

Arithmetic Sequence

a = ${a}, d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

Geometric Sequence

a = ${b}, r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

Notice how all arithmetic sequences look very similar: if the difference is positive, they steadily , and if the difference is negative, they steadily .

Geometric sequences, on the other hand, can behave completely differently based on the values of a and r:

If , the terms will , up to infinity. Mathematicians say that the sequence diverges.

If , the terms will always . We say that the sequence converges.

If , the terms will alternate between positive and negative, while their gets bigger.

You’ll learn more about convergence and divergence in the last section of this course.

Recursive and Explicit Formulas

In the previous section, you learned that a recursive formula tells you the value of each term as a function of previous terms. Here are the recursive formulas for arithmetic and geometric sequences:

xn=

One problem with recursive formulas is that to find the 100th term, for example, we first have to calculate the previous 99 terms – and that might take a long time. Instead, we can try to find an explicit formula, that tells us the value of the nth term directly.

For arithmetic sequences, we have to add d at every step:

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

At the nth term, we are adding copies of d, so the general formula is

xn=a+d×n−1.

For geometric sequences, we have to multiply r at every step:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

At the nth term, we are multiplying copies of r, so the general formula is

xn=a×rn−1.

Here is a summary of all the definitions and formulas you’ve seen so far:

An arithmetic sequence has first term a and common difference d between consecutive terms.

Recursive formula: xn=xn−1+d

Explicit formula: xn=a+d×n−1

A geometric sequence has first term a and common ratio r between consecutive terms.

Recursive formula: xn=xn−1×r

Explicit formula: xn=a×rn−1

Now let’s have a look at some examples where we can use all this!

Pay it Forward

Here is a short clip from the movie Pay it Forward, where 12-year-old Trevor explains his idea for making the world a better place:

The essence of Trevor’s idea is that, if everyone “pays it forward”, a single person can have a huge impact on the world:

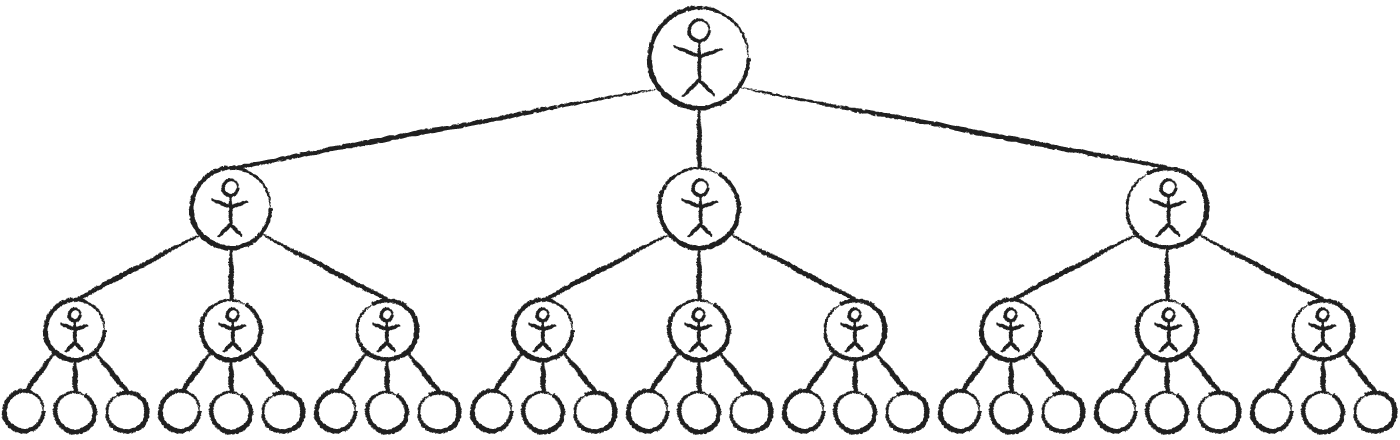
Notice how the number of people at every step forms a , with common ratio :

1, 3 ×3, 9 ×3, ×3, ×3, ×3, …

Using the explicit formula for geometric sequences, we can work out how many new people are affected at any step:

xn =

The number of people increases incredibly quickly. In the 10th step, you would reach 19,683 new ones, and after 22 steps you would have reached more people than are currently alive on Earth.

This sequence of numbers has a special name: the powers of 3. As you can see, every term is actually just a different power of 3:

30, 31, 32, 33, 34, 35, …

Who wants to be a Millionaire?

COMING SOON!

The Chessboard Problem

COMING SOON!

Sprache ändern

Melde dich bei Mathigon an

Teile

Fortschritt zurücksetzen

Glossar