Folgen und MusterFibonacci Numbers
Imagine that you’ve received a pair of baby rabbits, one male and one female. They are very special rabbits, because they never die, and the female one gives birth to a new pair of rabbits exactly once every month (always another pair of male and female).




















In the first month, the rabbits are very small and can’t do much – but they grow very quickly.
After one month, the rabbits are grown up and can start mating…
… and after another month, they will give birth to their first pair of kids. You now have two pairs of rabbits.
In the next month, your pair of rabbits will give birth to another couple. Meanwhile, the first pair of kids have grown up. You now have three pairs in total.
In the fifth month, your original pair of rabbits will give birth to a new pair. At the same time, their first pair of kids is now old enough to give birth to grandchildren. You now have five pairs of rabbits.
In the sixth month, there are three more couples that give birth: the original one, as well as their first two pairs or kids.
In the following month you would have 13 pairs of rabbits: the 8 ones from the previous month, plus 5 new sets of babies. Can you detect a pattern in this sequence?
The number of rabbits in a particular month is
Can you calculate the number of rabbits after a few more months?
1, 1, 2, 3, 5, 8,
So after 12 months, you’ll have 144 pairs of rabbits!
This sequence of numbers is called the
When Fibonacci was born in 1175, most people in Europe still used the
When he returned to Italy, Fibonacci wrote a book called Liber Abaci (Latin for “The Book of Calculations”), where he first introduced the new Arabic numerals to European merchants. They were an immediate success – and we still use them today.
On one of the pages in his book, he also investigated the breeding patterns of rabbits – that’s why the Fibonacci numbers were named after him.
Pages from Fibonacci’s Liber Abaci
Of course, the Fibonacci numbers are not how rabbits actually populate in real life. Rabbits don’t have exactly one male and one female offspring every single month, and we haven’t accounted for rabbits dying eventually.
But it turns out that there are many other places in nature where Fibonacci numbers do appear: for example the spirals in plants. Can you count how many spirals there are in each direction?
This pine cone has
This sunflower has 34 clockwise spirals and 55 counterclockwise spirals.
In both cases, the numbers of spirals are consecutive Fibonacci numbers. The same is true for many other plants: next time you go outside, count the number of petals in a flower or the number of leaves on a stem. Very often you’ll find that they are Fibonacci numbers!
Of course, this is not just a coincidence. There is an important reason why nature likes the Fibonacci sequence, which you’ll learn more about later.

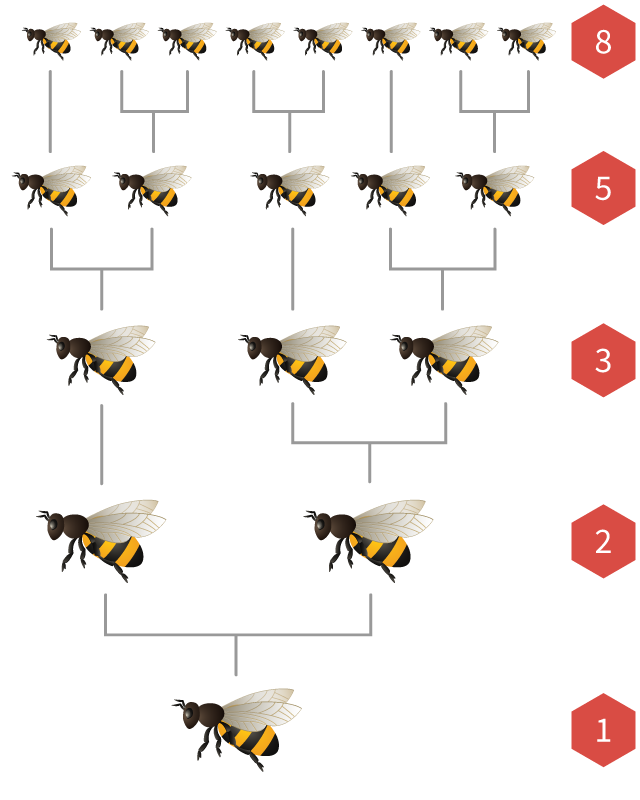
Fibonacci numbers also appear in the populations of honeybees.
In every bee colony there is a single queen that lays many eggs. If an egg is fertilised by a male bee, it hatches into a female bee. If it is not fertilised, it hatches into a male bee (called a drone).
This means that female bees have
If we draw the ancestry tree of a bee, the number of parents, grandparents, great-grandparents, and earlier generations are always Fibonacci numbers!
Occasionally, young female bees are fed with special food called “royal jelly”. In that case, they turn into queens and will fly away to start a new hive.
The Golden Ratio
Just like the
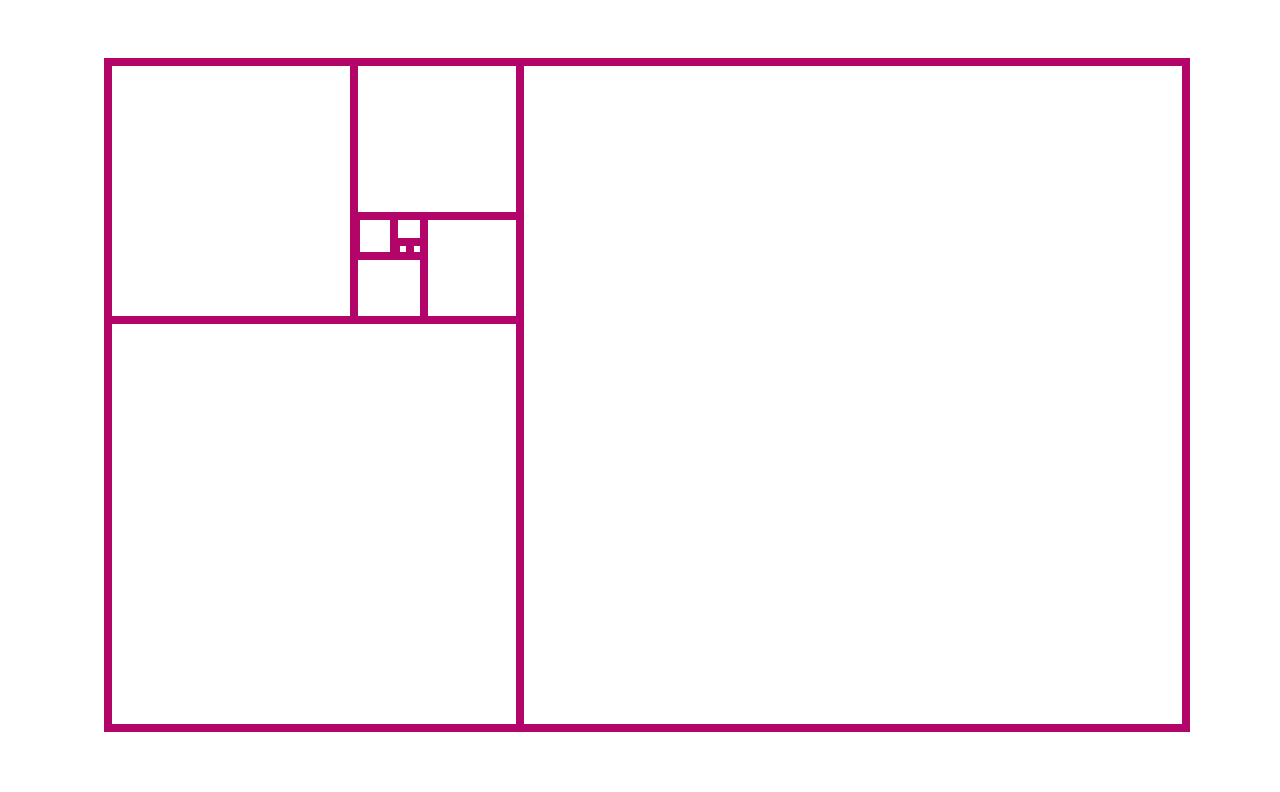
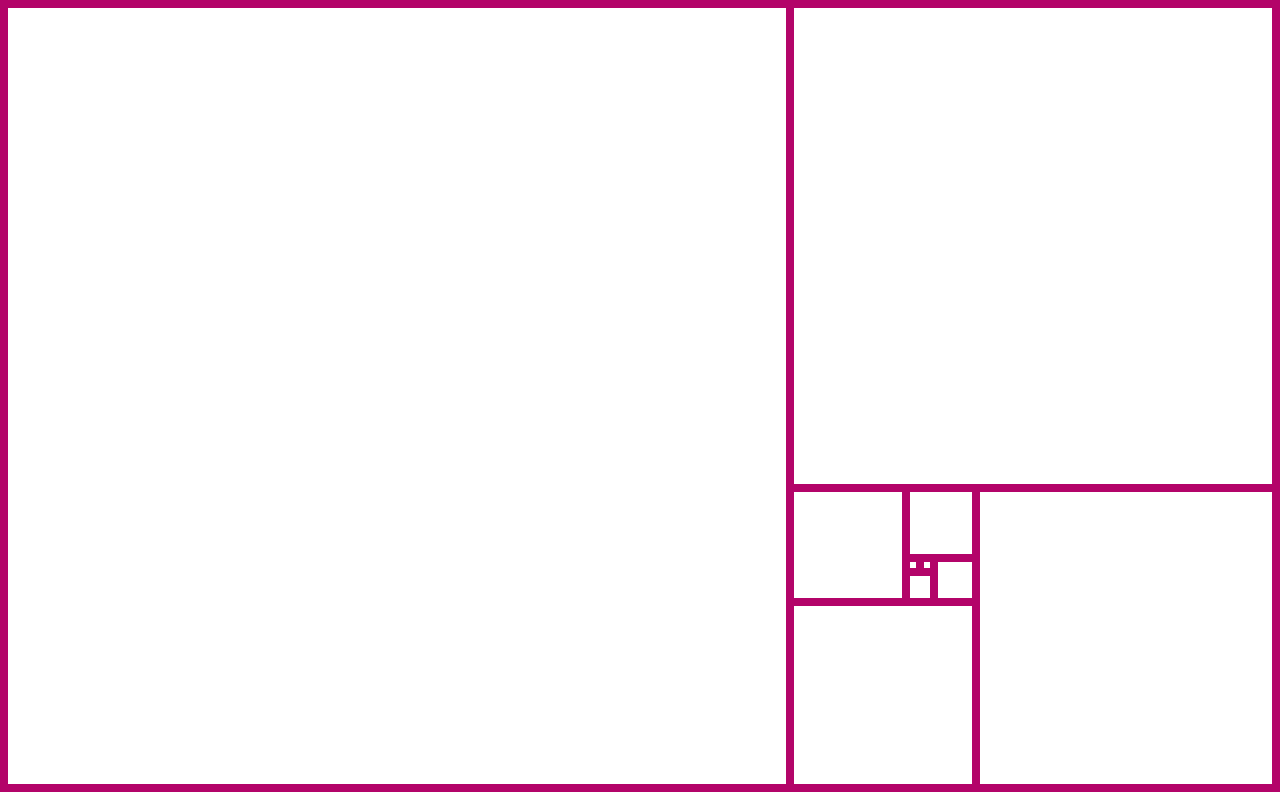
We start with two small squares of size 1.
Next, we add a new square of size 2, to form a larger rectangle.
Next, we add a square of size 3, to form an even larger rectangle.
The next square has size 5. Can you see that we’re recreating the Fibonacci numbers?
If we continue adding squares, they will have size 8, 13, 21, and so on.
You might have noticed that, as the rectangles get larger, they seem to start “spiraling” outwards. We can even visualise this by drawing a perfect spiral that connects the corners of the squares.
At every step, the squares form a larger rectangle. Its width and height are always two consecutive Fibonacci numbers. The aspect ratio of the rectangle is the ratio of its width and its height:
Notice how, as we add more and more squares, the aspect ratio seems to get closer and closer to a specific number around 1.6. This number is called the
Many people believe that the golden ratio is particularly aesthetically pleasing. That’s why it is often used by artists and architects – like in these two examples:
The Greek sculptor Phidias is said to have used the golden ratio when designing the Parthenon in Athens. The first letter of his name,
The Sacrament of the Last Supper, by Spanish artist Salvador Dalí, is one of many paintings in the golden ratio. In the background, you can also see a large
We can approximate the golden ratio by
However, it turns out that the exact value of
Fibonacci Spirals
The golden ratio explains why Fibonacci numbers appear in nature, like the sunflower and pine cone you saw at the beginning of this section.
Both these plants grow outwards from their center (a part of the plant called the meristem). As new seeds, leaves or petals are added, they push the existing ones further outwards.
Move the slider on the right to visualise how a plant grows. Notice how every leaf is added at a different rotation than the previous one. The angle between two consecutive leafs is always the same.
It is important for flowers to pick a suitable angle: the leaves or seeds have to be approximately equally spaced so that they get the largest amount of sunlight and nutrients. In the diagram below, you can explore what a sunflower might look like with different angles between its seeds:
If the angle is , all seeds will grow in a single long row away from the center.
If the angle is of a full a rotation (180°), the seeds will alternate between two separate “arms” that move away from the center.
If the rotation is another fractional proportion of 360°, for example or or , then the number of “arms” will be the same as the
Unfortunately “arms” are bad, because they mean that the seeds are not evenly distributed: all of the space between the arms is wasted. But if
One example of an irrational number is
It turns out that the
You might remember from above that the ratios of consecutive Fibonacci numbers get closer and closer to the golden ratio – and that’s why, if you count the number of spirals in a plant, you will often find a Fibonacci number.
It is important to remember that nature doesn’t know about Fibonacci numbers. Nature also can’t solve equations to calculate the golden ratio – but over the course of millions of years, plants had plenty of time to try out different angles and discover the best one.
Plants and animals always want to grow in the most efficient way, and that is why nature is full of regular, mathematical patterns.
Fibonachos
So far, we have only used the recursive equation for Fibonacci numbers. There actually is an explicit equation, too – but it is much more difficult to find:
We could also try picking different starting points for the Fibonacci numbers. For example, if we start with 2, 1, … rather than 1, 1, … we get a sequence called the Lucas numbers.
It turns out that, whatever two starting numbers you pick, the resulting sequences share many properties. For example, the ratios of consecutive terms will always
There are many other puzzles, patterns and applications related to Fibonacci numbers. Here are a few examples, which you can try yourself:
Problem solving
1. Fibonacci Divisibility
(a) Which Fibonacci numbers are even? Is there a pattern to where they are positioned along the sequence? Can you explain why?
(b) Which Fibonacci numbers are divisible by 3 (or divisible by 4)? What do you notice?
2. Fibonacci Sums
What happens if you add up any three consecutive Fibonacci numbers? Can you explain why?
3. Fibonacci Staircases
When walking up the stairs, I can either take single steps or leap over two steps at a time. This means that there are many different possibilities for how I could go up a staircase. For example, if there are 5 steps, I have 8 different choices:
How many choices are there for staircase with 6, 7 or 8 steps? Can you detect a pattern? And how is this related to the Fibonacci numbers?
© FoxTrot, by Bill Amend