Abbildungen und SymmetrieSymmetriegruppen und Muster
Einige Formen haben mehr als eine Symmetrie - schauen wir uns das








Du hast bereits oben gezeigt, dass ein Quadrat
Es ist auch rotationssymmetrisch und zwar um
Und schließlich können wir uns als eine weitere besondere Art der Symmetrie das "Nichts tun" vorstellen - denn das Ergebnis ist (eh klar) das gleiche wie zuvor. Dies wird manchmal als die Identität bezeichnet.
Insgesamt haben wir
Jetzt können wir tatsächlich anfangen, mit diesen Symmetrien zu rechnen. Zum Beispiel können wir zwei Symmetrien addieren , um neue zu erhalten:






Immer wenn man zwei Symmetrien eines Quadrats addiert, erhält man eine neue. Hier ist ein "Symmetrie-Rechner", mit dem du das selbst ausprobieren kannst:
Verbringe einige Zeit damit, mit dem Symmetrie-Rechner herumzuspielen, und versuche, irgendwelche gemeinsame Muster zu finden. Kannst du diese Beobachtungen vervollständigen?
- Das Addieren von zwei Drehungen ergibt immer eine
(oder die Identität). - Das Addieren von zwei Spiegelungen ergibt immer eine
(oder die Identität). - Das Addieren zweier Symmetrien in umgekehrter Reihenfolge ergibt
Ergebnis. - Die Addition der Identität
.
Du hast vielleicht schon bemerkt, dass das Addieren von Symmetrien eigentlich dem Addieren von ganzen Zahlen sehr ähnlich ist:
- Die Addition von zwei Symmetrien/ganzen Zahlen ergibt immer eine andere Symmetrie/ganze Zahl:
+ = 12 + 7 = 19 - Die Addition von zwei Symmetrien/ganzen Zahlen ist
assoziativ :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Jede Symmetrie/ganze Zahl hat eine inverse, eine andere Symmetrie/ganze Zahl die, wenn man sie dazu addiert, die Identität ergibt:
+ = 4 + -4 = 0
In der Mathematik wird jede Menge von Elementen, die diese Eigenschaften hat, als
In diesem Beispiel haben wir mit den acht Symmetrien des Quadrats begonnen. Tatsächlich hat jede geometrische Form ihre eigene Symmetriegruppe. Sie alle haben unterschiedliche Elemente, aber sie erfüllen immer die drei obigen Regeln.
Gruppen erscheinen überall in der Mathematik. Die Elemente können Zahlen oder Symmetrien sein, aber auch Polynome, Permutationen, Matrizen, Funktionen … alles , was die drei Regeln erfüllt. Die Grundidee der Gruppentheorie ist, dass wir uns nicht für die einzelnen Elemente interessieren, sondern nur dafür, wie sie sich gegenseitig beeinflussen.
So können beispielsweise die Symmetriegruppen verschiedener Moleküle den Wissenschaftlern helfen, die Eigenschaften der entsprechenden Materialien vorherzusagen und zu erklären.
Gruppen können auch verwendet werden, um die Gewinnstrategie in Brettspielen, das Verhalten von Viren in der Medizin, verschiedene Harmonien in der Musik und viele andere Konzepte zu analysieren…
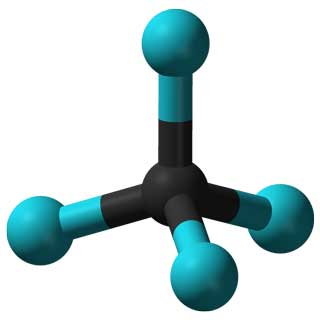
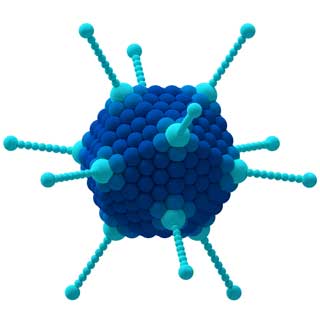
Die Eigenschaften des CCl4-Moleküls (links) und des Adenovirus (rechts) werden durch ihre Symmetrien bestimmt.
Ornamentgruppen
Im vorigen Kapitel haben wir zwei verschiedene Arten von Symmetrie gesehen, die zwei verschiedenen Abbildungen entsprechen: Drehungen und Spiegelungen. Aber es gibt auch eine Symmetrie für die dritte Art der Kongruenzabbildung:


Sechseckige Honigwaben


Keramische Wandfliesen
Neben der Spiegelungs-, Rotations- und Verschiebungssymmetrie gibt es sogar eine vierte Art:


Ein Muster kann auch mehr als eine Symmetrieart aufweisen. Und, genau wie bei den Quadraten, können wir die
Diese Gruppen sagen wenig darüber aus, wie das Muster aussieht (z.B. seine Farben und Formen), man erfährt nur wie es sich wiederholt. Mehrere verschiedene Muster können die gleiche Symmetriegruppe haben - vorausgesetzt, sie werden auf die gleiche Weise angeordnet und wiederholt.


Diese beiden Muster haben die gleichen Symmetrien, auch wenn sie sehr unterschiedlich aussehen. Bei Symmetrien geht es aber nicht um Farben oder oberflächliche Formen.


Diese beiden Muster haben auch die gleichen Symmetrien - auch wenn sie den entsprechenden Mustern auf der linken Seite ähnlicher sind als einander.
Es stellt sich heraus, dass es zwar unendlich viele mögliche Muster gibt, sie aber alle eine von nur 17 verschiedenen Symmetriegruppen haben. Diese werden als Ornamentgruppen bezeichnet. Jede Ornamentgruppe wird durch eine Kombination von Verschiebungen, Drehungen, Spiegelungen und Gleitspiegelungen definiert. Kannst du in diesen Beispielen die

Gruppe 1 - p1
Nur Verschiebungen

Gruppe 2 - p2
zweizählige Drehung, Verschiebungen

Gruppe 3 - p3
Dreizählige Drehungen (120°), Verschiebungen

Gruppe 4 - p4
Vier zweizählige Drehungen (180°), Verschiebungen

Gruppe 5 - p6
Zwei-, drei- und sechszählige Drehungen (60°), Verschiebungen

Gruppe 6 - PM
Parallele Spiegelachsen, Verschiebungen

Gruppe 7 - PMM
Senkrechte Spiegelungen, zweizählige Drehungen, Verschiebungen

Gruppe 8 - P4M
Drehungen (2 + 4), Spiegelungen, Gleitspiegelungen, Verschiebungen

Gruppe 9 - P6M
Drehungen (2 + 6), Spiegelungen, Gleitspiegelungen, Verschiebungen

Gruppe 10 - P3M1
Drehungen (3), Spiegelungen, Gleitspiegelungen, Verschiebungen

Gruppe 11 - P31M
Drehungen (3), Spiegelungen, Gleitspiegelungen, Verschiebungen

Gruppe 12 - P4G
Drehungen (2 + 4), Spiegelungen, Gleitspiegelungen, Verschiebungen

Gruppe 13 - CMM
Senkrechte Spiegelungen, Drehungen (2), Verschiebungen

Gruppe 14 - PMG
Spiegelungen, Gleitspiegelungen, Drehungen (2), Verschiebungen

Gruppe 15 - PG
Parallele Gleitspiegelungen, Verschiebungen

Gruppe 16 - CM
Spiegelungen, Gleitspiegelungen, Verschiebungen

Gruppe 17 - PGG
Senkrechte Gleitspiegelungen, Drehungen (2), Verschiebungen
Leider ist der Grund dafür, warum es genau 17 dieser Gruppen gibt, nicht einfach. Der Beweis dafür erfordert eine viel fortgeschrittenere Mathematik…
Stattdessen kannst du versuchen, deine eigenen sich wiederholenden Muster für jede der 17 Ornamentgruppen zu zeichnen:
Beispiele von Zeichnungen anderer Schüler



Bei den Ornamentgruppen ging es um ebene, zweidimensionale Muster. Bei dreidimensionalen Mustern können wir etwas Ähnliches tun : Man nennt sie kristallographische Raumgruppen, und es gibt 219 davon!
Zu diesen Gruppen gehören neben Verschiebungen, Spiegelungen, Drehungen und Gleitspiegelungen auch Symmetrien wie Gleitebenen und Schraubungen (stelle dir die Bewegung beim Aufschrauben einer Flasche vor).
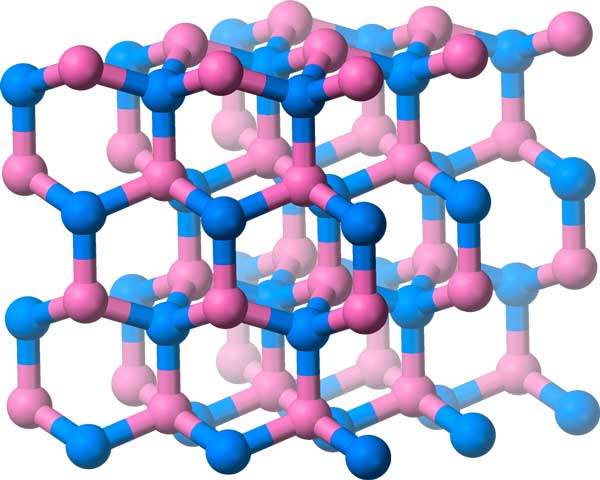
In diesem Kristallgitter, das eine dreidimensionale Symmetriegruppe aufweist, sind die Moleküle von Bornitrid angeordnet.