Vielecke und PolyederParkettierung (Tessellation)

Vielecke treten überall in der Natur auf. Sie sind besonders nützlich, wenn man eine große Fläche kacheln möchte, da man Vielecke ohne Lücken oder Überlappungen zusammenfügen kann. Solche Muster werden als Parkettierungen bezeichnet.

Die Menschen haben viele dieser natürlichen Muster in Kunst, Architektur und Technik kopiert - vom alten Rom bis in die Gegenwart. Hier sind einige Beispiele:

Hier kannst du deine eigenen Parkettierungen mit regelmäßigen Vielecken erstellen. Ziehe einfach neue Formen aus der Seitenleiste auf die Leinwand. Welche Formen eignen sich gut für Parkettierungen? Gibt es Formen, die sich nicht kacheln lassen? Versuche, interessante Muster zu erstellen!

Beispiele für die Parkettierungen anderer Studenten

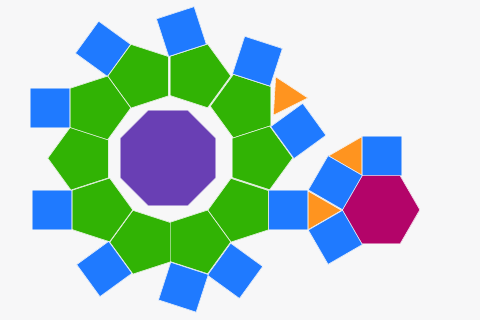
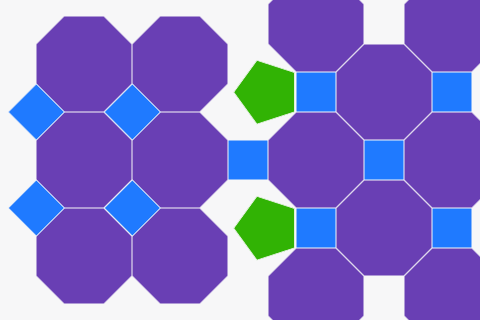
Parkettierungen mit regelmäßigen Vielecken

Du hast vielleicht bemerkt, dass sich einige regelmäßige Vielecke (wie QuadrateFünfecke) sehr gut und andere (wie FünfeckeDreieckeSechsecke) sich überhaupt nicht für Parkettierungen eignen.

Das hat mit der Größe ihrer Innenwinkelzu tun, mit deren Berechnung wir uns schon beschäftigt haben. An jedem Eckpunkt in dieser Parkettierung treffen sich die Innenwinkel mehrerer verschiedener Vielecke. Alle diese Winkel müssen zusammengezählt ergeben, sonst gibt es entweder eine Lücke oder eine Überlappung.

Du kannst auch überprüfen, dass, genau wie bei Fünfecken, jedes normale Vieleck mit 7 oder mehr Seiten keine Parkettierung ergibt. Das bedeutet, dass die einzigen regelmäßigen Vielecke, die Parkettierungen ermöglichen, Dreiecke, Quadrate und Sechsecke sind!

Natürlich kann man auch verschiedene Arten von regelmäßigen Vielecken in einer Parkettierung kombinieren, vorausgesetzt, ihre Innenwinkel ergeben in Summe 360°:

Quadrate und Dreiecke
90° + 90° + 60° + 60° + 60° = 360°

Quadrate und Dreiecke
90° + 90° + 60° + 60° + 60° = 360°

Sechsecke und Dreiecke
120° + 120° + 60° + 60° = 360°

Sechsecke und Dreiecke
120° + 60° + 60° + 60° + 60° = 360°

Sechsecke, Quadrate und Dreiecke
120° + 90° + 90° + 60° = 360°

Achtecke und Quadrate
135° + 135° + 90° = 360°

Zwölfecke (Dodekagone) und Dreiecke
150° + 150° + 60° = 360°

Zwölfecke, Sechsecke und Quadrate
150° + 120° + 90° = 360°

Parkettierungen mit unregelmäßigen Vielecken

Wir können auch versuchen, Parkettierungen aus unregelmäßigen Vielecken herzustellen - vorausgesetzt, wir passen beim Drehen und Anordnen gut auf.

Fünfecke sind etwas kniffliger. Wir haben bereits gesehen, dass regelmäßige Fünfecke sich nicht gut für Parkettierungen eignen. Aber was ist mit unregelmäßigen Fünfecken?

Hier sind drei verschiedene Beispiele für Parkettierungen mit Fünfecken. Sie sind nicht regelmäßig, aber sie sind einwandfreie fünfseitige Vielecke.

Bisher haben Mathematiker nur 15 verschiedene Arten von Parkettierungen mit (konvexen) Fünfecken gefunden - die jüngste davon wurde 2015 entdeckt. Niemand weiß, ob es noch andere gibt, oder ob diese 15 die einzigen sind…

Parkettierungen in der Kunst

Parkettierungen sind für viele Künstler, Architekten und Designer ein Werkzeug und eine Inspiration - allen voran der niederländische Künstler M. C. Escher. Eschers Werk enthält seltsame, mutierende Kreaturen, Muster und Landschaften:

Diese Kunstwerke sehen oft spaßig und mühelos aus, aber die zugrunde liegenden mathematischen Prinzipien sind die gleichen wie zuvor: Winkel, Rotationen, Translationen und Vielecke. Wenn die Mathematik nicht stimmt, wird die Parkettierung nicht funktionieren!

“Metamorphose II” von M. C. Escher (1940)

Penrose-Parkettierungen

Alle bisherigen Parkettierungen haben eines gemeinsam: Sie sind periodisch. Das heißt, sie bestehen aus einem regelmäßigen Muster, das immer wieder wiederholt wird. Sie können auf ewig in alle Richtungen weitergehen und werden überall gleich aussehen.

In den 1970er Jahren entdeckte der britische Mathematiker und Physiker Roger Penrose nicht-periodische Parkettierungen - sie gehen immer noch unendlich in alle Richtungen weiter, sehen aber nie genau gleich aus. Diese werden als Penrose-Parkettierungen bezeichnet, und man benötigt nur ein paar verschiedene Arten von Vielecken, um sie zu erstellen:

Penrose untersuchte Parkettierungen nur zum Spaß, aber es stellte sich heraus, dass die innere Struktur einiger echter Materialien (wie Aluminium) einem ähnlichen Muster folgt. Das Muster wurde sogar auf Toilettenpapier verwendet, da die Hersteller feststellten, dass ein nicht-periodisches Muster ganz glatt aufgerollt werden kann.